其他技术

本章开发的每一项技术都有其自身的价值，但这还是我解释它们的唯一原因。更主要的是让你熟悉一些在神经网络里会出现的问题，和一种可以帮你解决这些问题的分析方式。某种意义上，我们一直在学习如何理解神经网络。本章剩余部分我简短的概述下一些其他有用的技术。这些概述要比之前的讨论少一些尝试，但会表达这样一种感觉，在神经网络的应用中是有多种多样技术的。

随机梯度下降算法的变种

通过反向传播，随机梯度下降算法已经为我们很好的解决了MNIST数字分类问题。然而，有很多其他方法来优化成本函数，有时这些其他方法会提供比小批次梯度下降算法更好性能。本节我概述两种这样的方法，Hessian和动量技术。

Hessian技术：在开始我们的讨论之前，先把神经网络放一边。反而我们只去考虑最小化一个成本函数$C$这个抽象问题，这个函数有很多变量，$w = w_1, w_2, \ldots$，所以有$C = C(w)$。由泰勒定理，成本函数可以近似接近于一个点$w$通过

$\begin{eqnarray} C(w+\Delta w) & = & C(w) + \sum_j \frac{\partial C}{\partial w_j} \Delta w_j \nonumber \\ & & + \frac{1}{2} \sum_{jk} \Delta w_j \frac{\partial^2 C}{\partial w_j \partial w_k} \Delta w_k + \ldots \tag{103} \end{eqnarray}$

我们可以写的更简洁一点

$\begin{eqnarray} C(w+\Delta w) = C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w + \ldots, \tag{104} \end{eqnarray}$

这里$\nabla C$是平常的梯度向量，$H$是一个矩阵被称为$Hessian矩阵$，其中第$jk$个实体是$\partial^2C / \partial w_j \partial w_k$。假设我们通过丢弃上面有$\ldots$表示的高阶项来对$C$进行近似，

$\begin{eqnarray} C(w+\Delta w) \approx C(w) + \nabla C \cdot \Delta w + \frac{1}{2} \Delta w^T H \Delta w. \tag{105} \end{eqnarray}$

通过微积分可以证明右手边的公式可以最小化【严格的讲，这里的最小化，不仅是一个极限，我们要假设Hessian矩阵是正数。直观上讲，这意味着函数$C$看上去像一个山谷的局部，不是一座山峰或马鞍。】通过选

$\begin{eqnarray} \Delta w = -H^{-1} \nabla C. \tag{106} \end{eqnarray}$

假设(105)是对成本函数很好的近似，那么我们期望从$w$点移到$w+\Delta w = w-H^{-1} \nabla C$会显示的减小成本函数。这导出了一个最小化成本的可能算法：

• 选择一个起始点，$w$。

• 更新$w$ 到一个新点$w' = w-H^{-1} \nabla C$，这里的Hessian$H$和$\nabla C$是根据$w$算出来的。

• 更新$w'$到一个新的点$w{'}{'} = w'-H'^{-1} \nabla' C$，这里的Hessian $H'$和$\nabla 'C$是根据$w'$算出来的。

• $\ldots$

实际上，（105）只是一个近似，最好迈的步子能小一点。我们这样重复的按一定的量$\Delta w = -\eta H^{-1} \nabla C$来改变$w$，其中$\eta$就是学习率。

这种最小化成本函数的方法叫做Hessian技术或Hessian优化。理论和时间表明Hessian方法收敛到最小值要比随机梯度下降法的步数要少。尤其是Hessian方法在成本函数中加入了二阶变化的信息，可以避免许多梯度下降算法出现的问题。此外，有多个反向传播算法的版本可以用来计算Hessian。

如果Hessian优化这么厉害，为什么没有用在我们的神经网络里呢？不幸的是，虽然它有许多很不错的特性，但有一个很糟糕的性质：很难应用于实践中。部分问题是的Hessian矩阵的绝对大小。假设你的神经网络有$10^7$个权重和偏移量。那么对应的Hessian矩阵将包含$10^7 \times 10^7 = 10^{14}$个实体。这么多实体！将导致在实际过程中计算$H^{-1} \nabla C$格外困难。尽管这样也不是说理解它没有用处。实事上，有很多梯度下降的变种是受到Hessian优化的启发，但要去避免超大矩阵的问题。让我们来看一个这样的技术，基于动量的梯度下降算法。

基于动量的梯度下降算法：直观上讲，Hessian优化的优点在于它不仅整合了梯度信息，还有梯度变化的信息。基于动量的梯度下降算法也是基于与之相似的思想，但避免了二阶导数的超大矩阵问题。为了理解动量技术，回想一下我们梯度下降的原始图像，里面我们将其看成是一个球滚到山谷里。当然是我们看到，虽然名字叫梯度下降，但只是不严谨的类比于一个球滚动谷底。动量技术对梯度下降做了两处修改，让其与实图上的更相似。首先，它引进了一个概念，也是需要优化的参数——“速度”。梯度的要做的是去改变速度，而不是（直接）改变“位置”，就像物理中的力改变速度，也只是间接影响位置而以。第二点是，动量方法引进了一类摩擦力项，让其趋向于逐渐减小速度。

让我们看一个更精确的数学描述。我们引入速度变量$v = v_1, v_2, \ldots$，每一个对应$w_j$变量【当然，在神经网络里$w_j$变量，会包含所有的权重和偏移量】。然后我们将梯度下降更新规则$w \rightarrow w'= w-\eta \nabla C$替换为

$\begin{eqnarray} v & \rightarrow & v' = \mu v - \eta \nabla C \tag{107}\\ w & \rightarrow & w' = w+v'. \tag{108} \end{eqnarray}$

这些公式里面，$\mu$是一个控制系统中阻尼或摩擦系数量的超参数。为了理解公式的含义，首先看一下$\mu = 1$的情况，也就是没有摩擦。这种情况下，代入后的公式表明，“力”$\nabla C$现在改着速度，$v$，而速度控制着$w$的变化率。直观上讲，我们通过重复加梯度项来构建这个速度。这就意味着如果梯度是（大致上）在同一方向上的，经过多个回合的学习，我们可以在这个方向上前进很远。例如，想下如果我们笔直沿斜坡下降会发生什么：

每一步在斜坡下降的速度会越来越大，所以我们越来越快地移动到谷底。这让动量技术比较梯度下降更有效率。当然，一个问题是一旦我们到达谷底，我们会越过目标。或者如果梯度变化的太快，我们会发现自己在错误的方向上移动。这就是(107)里$\mu$这个超参数存在的原因。我前面说过$\mu$是系统里控制摩擦系数的；为了更精确一点，你应该将系统的摩擦系数$\mu$理解为1。正如我们看到的，当$\mu = 1$时，没有摩擦，速度完全由梯度$\nabla C$主导。相对的，当$\nabla = 0$时有很大的摩擦，速度起不来，公式(107)和(108)变为平常的梯度下降公式，$w \rightarrow w'=w-\eta \nabla C$。实践上，$\mu$用一个$0$和$1$的中间值可以在构建速度方面带来很多益处，还不会导致越过目标。我们可以用保留出的验证数据来$\mu$挑选这样一个值，和选$\eta$和$\lambda$的方式很像。

到目前为止，我避免去命名$\mu$这个超参数。原因是$\mu$的标准名称起得很不好：它被称为动量系数。这会让人产生歧义，因为$\mu$根本和物理中的动量不是一回事。不如说它更接近于摩擦系数。尽管如此动量系数这个术语已经应用的很广泛了，所以我们将继续用它。

对于动量技术来说一个非常消息是，修改一个梯度下降算法的实现去包含动量几乎不费吹灰之力。我们仍然可以和之前一样，用反向传播算法来云计算梯度，并用诸如随机采样的思想来挑选小批次。用这种方式我们可以得到许多Hessian技术上的优点，使用的是关于梯度变化的信息。但它没有其缺点，且对代码实现只是稍作修改。实践上，动量技术被应用广泛，通常会使用学习更有效率。

练习

• 如果我们在动量技术里用$\mu > 1$为什么出现错误？

• 如果我们在动量技术里用$\mu < 0$为什么出现错误？

问题

• 添加基于动量的随机梯度下降算法到network2.py。

其他最小化成本函数的算法：许多其他最小化成本函数的方法被设计出来，哪一个是最好的方法还没有统一的定论。你研究神经网络越深入就越值得去挖掘其他技术，理解它们的工作原理，它们的强项和弱点，和怎样将它们应用到实践中。我之前提到一篇论文【Efficient BackProp, 作者 Yann LeCun, Léon Bottou, Genevieve Orr 和Klaus-Robert Müller (1998)】介绍并比较了许多这样的技术，包换结合了梯度下降和BFGS的方法（还可以看到与之密切相关的有限内存BFGS方法，即L-BFGS）。另一个最近展示出不错结果【例子可以看On the importance of initialization and momentum in deep learning, 作者 Ilya Sutskever, James Martens, George Dahl, 和 Geoffrey Hinton (2012)】的技术是 Nesterov 的梯度加速技术，它在动量技术上做了改进。尽管这样，对于许多问题，普通的随机梯度下降算法做的很好，特别是如果用了动量的话，所以我们将在本章余下的内容里坚持使用随机梯度下降算法。

其他神经元模型

目前为止我们都是用sigmoid神经元来构建神经网络的。原则上用sigmoid神经元构建的网络可以计算任何函数。尽管这样，实践过程中，用其他神经元模型构建的网络有时要比sigmoid网络好很多。依赖于具体应用，基于这种这种替换后的模型可能学习的更快，在测试数据上泛化的更好，又或两者兼具。让我们提一对神经元的替换模型，让你看一些通常使用东西的变种。

大概最简单的变种就是tanh(发音“tanch”) 神经元，将sigmoid函数替换成正切双曲线函数。在输入为$x$，权重向量为$w$和偏移量为$b$的tanh神经元的输出为

$\begin{eqnarray} \tanh(w \cdot x+b), \tag{109} \end{eqnarray}$

当然这里的tanh是一个双曲线正切函数。事实证明这与sigmoid神经元是非常接近。为了明白这句话的意思，回想tanh函数的定义

$\begin{eqnarray} \tanh(z) \equiv \frac{e^z-e^{-z}}{e^z+e^{-z}}. \tag{110} \end{eqnarray}$

使用一点代数知识可以证明

$\begin{eqnarray} \sigma(z) = \frac{1+\tanh(z/2)}{2}, \tag{111} \end{eqnarray}$

也许就是说，tanh只是一个缩放版本的sigmoid函数。我们也可以从图形中看到，tanh函数有着与sigmoid函数相似的形状，

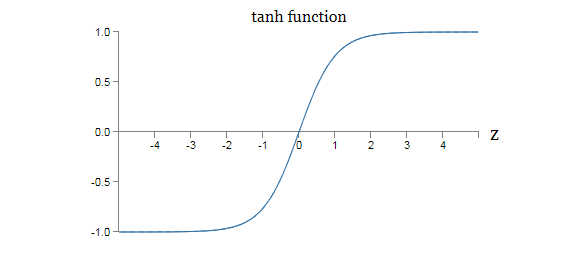
tanh函数和sigmoid函数间的一个不同就是，tanh神经元的输出范围是从$-1$到$1$，而不是$0$到$1$。这就意味着如果你要基于tanh神经元去搭建一个网络，你可能需要去归一化你的输出（并且，依赖于具体的应用，可能还有你的输入），这是一点与sigmoid函数小小的不同。

与sigmoid函数相似的，tanh函数的网络原则上也可以计算任何函数【对于tanh和sigmoid神经元，以及下面讨论的修正的线性神经元，还有一些技术上警告声明。尽管这样通俗的讲神经网络可以将任何函数近似于任意精度】，将输入映射到范围$-1$到$1$。此外，像反向传播和随机梯度下降的思想，可以很容易的从sigmoid神经元网络应用至tanh神经元的网络中。

练习

• 证明公式(111)是恒等的。

那在网络里该用哪种神经元，tanh还是sigmoid？婉转的说先天的答案并不明显！尽管这样，有理念证明和一些实际证据给出tanh有时更好一些【例子可以看 Efficient BackProp, 作者 Yann LeCun, Léon Bottou, Genevieve Orr 和 Klaus-Robert Müller (1998), 还有 Understanding the difficulty of training deep feedforward networks, 作者 Xavier Glorot 和 Yoshua Bengio (2010)】。让我简单介绍一下tanh神经元的理论证明。假设我们正在用的是sigmoid神经元，因此所有的激活值是正的。我们看下第$l + 1$层第$j$个神经元的权重输入$w^{l+1}_{jk}$。反向传播的规则（看这里）告诉我们对应的梯度将会是$a^l_k \delta^{l+1}_j$。因为激活值是正数，所以梯度的正负将和$\delta^{l+1}_j$的正负相同。这就意味着如果$\delta^{l+1}_j$是正数，那么所有的权重$w^{l+1}_{jk}$将在梯度下降期间减小，而如果$\delta^{l+1}_j$是负数，那么所有的权重$w^{l+1}_{jk}$在梯度下降期间增加。换句话说，同一神经元的所有权重要么一起增加，要么一起减小。这就产生了一个问题，因为当其他一些权重需要减小的同时，一些权重可能需要增加。这只有在输入激活有不同正负号的情况下才会发生。这就指出要用像tanh这样的激活函数来替换sigmoid，它同时允许正数和负数的激活值。的确，因为tanh是关于0对称的，$\tanh(-z) = -\tanh(z)$，我们可能甚至期望这样的性质，粗略的讲，隐含层里的激活值将在正负间很均衡。这会帮我们确保对权重的更新没有系统性的偏见。

我们要怎样对待这一说法？虽然这个说法有一定的建设性，但也只是一个启发，而不一个严格证明，说tanh神经元要好过sigmoid神经元。或许sigmoid神经元有其他性质补偿了这个问题？确实是这样，根据经验对许多任务，在性能上tanh比sigmoid神经元只有很小或根本没有提升。不幸的是,对于任何实际问题，我们还没有固定的规则来知道哪种神经元会学的更快，或有更好的泛化能力。

别一个sigmoid神经元的变种是线性整流神经元(rectified linear neuron)或线性整流函数(rectified linear unit)。对于输入为$x$，权重向量为$w$和偏移量为$b$的一个线性整流函数的输出为

$\begin{eqnarray} \max(0, w \cdot x+b). \tag{112} \end{eqnarray}$

形象地说整流函数$\max(0, z)$看起来像是这样：

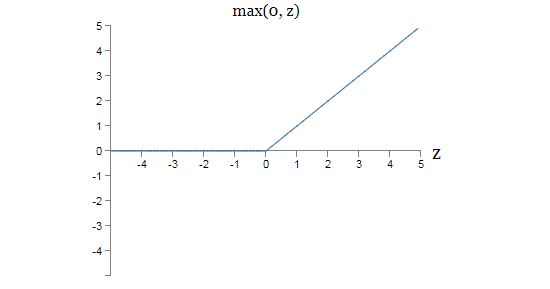
乍一看这个神经元与sigmoid和tanh神经元区别很大。尽管这样，像sigmoid和tanh神经元一样，线性整流函数可以用来计算任何函数，并且它们可以用诸如反向传播和随机梯度下降的思想来进行训练。

什么时候需要用线性整流函数来替换sigmoid或tanh神经元呢？近来在图像识别上的一些工作发现，使用线性整流函数的很多网络都显著的收益。尽管如此，和tanh神经元一样，我们还没有真正深入理解，什么时候线性整流函数确保会更好，更不用说为什么了。为了给你看一些问题，回想sigmoid神经元当饱和时会停止学习，也就是当它们的输出接近$0$或$1$里。本章我们已经重复说过多次，问题的原因是$\sigma'$项减小了，导致了学习缓慢。tanh神经元在饱和时会遇到一样的问题。相对的，对一个线性整流函数增加权重输入永远不会引起饱和，因此也不会有学习缓慢的问题。另一方面，当然一个线性整流函数的权重输入是负数时，梯度消失，导致神经元彻底停止了学习。这只是在众多问题中的两个，让我们很理解什么时候和为什么线性整流函数要比sigmoid或tanh神经元更好。

这里我定了个不确定的基调，主要是想说我们还有一个固定的关于该如何挑选激活函数的理论。的确，这个问题甚至要比我描述的更加困难，因为有无限多个可能的激活函数。对于任意给出的问题该选哪一个？哪一个的网络学习的最快？哪一个的测试准确率最高？我很惊讶，对于这些问题真正有深度和系统性的研究如此之少。理想中，我们应该有一个理论详细的告诉我们该怎样去挑选（也可能是动态修改）激活函数。另一方面，我们不应该因为没有一套完整的理论就停下脚步！我们手边有强力的工具，而且用这些工具可以取得很大的进展。本书的剩余部分，我将继续用sigmoid做为我们神经元的首选，因为它们很强大，而且提供了关于神经网络核心思想的具体特征。但请记住这些相同的思想可以被应用到其他类型的神经元上，并且有时这样做会有提升。

关于神经网络的故事

问题： 你是如何使用和研究机器学习技术的，它完全是凭经验，而不数学？同时你注意过在何种情况下其中一些技术是没用的？

回答：你已经注意了我们的理念工具是非常弱的。有时我们有很好的数学上的直觉来解释为什么一个特定技术会有效。有时我们的直觉最终是错的[...]那问题就变成：我的方法在特定问题上效果如何，和它能在多大范围的问题领域上是有效的。

• 问与答 作者 神经网络研究者Yann LeCun

有一次参加一个量子力学的会议，我注意一个非常有意思的语言习惯：当演讲结果后，观众们的问题通常会用这句话开头“我很赞同你的观点，但[...]”。量子力学不是我平时的领域，并且我注意到这种形式的问题，是因为在其他学术会议上，我很少或从未听过一个提问者表达他们赞同演讲者的观点。当时，我想这个问题很普遍指出，在量子力学方面大家的进展有限，大家仅仅都是在重复发明轮子。后来，我认识这种评价太苛刻了。演讲者正在与人类意识中遇到的最困难的问题做搏斗。进展当然不会很快！但还是值得听一听大家的最新想法，即使他们并不总是有突破性的进展来做报告。

你可以已经注意到在本书中也有类似这样的语言表达“我非常赞同[...]”。为了解释我们所看到的，我通常会退一步说“根据经验来说，[...]”，或“粗略的讲，[...]”，接上一个故事来解释一些现象或其他东西。这些故事是可信的，但我提出的实际证据通常底气不足。如果你浏览下参考文献，你会发现在其他很多神经网络的研究论文也是用类似的方式在讲故事，通常都是没有足够的证据支撑。我们该对这些故事怎么想呢？

在科学的许多方面——尤其是那些处理简单现象的部分——对于一般的假设，可能可以得到非常固定非常可靠的证据的。但在神经网络里有大量的参数和超参数，而且它们之间的相互作用非常复杂。在这种极其复杂的系统中，要建立可靠的一般性声明是极其困难的。理解神经网络的通用性是一个问题，就像量子力学在测试人类意识的极限。结果就是这些声明有时需要在新的证据出现后作修改或抛弃。

一种看待这种情况的方式是，任何有启发性关于神经网络的故事都承载着一个隐含的挑战。举个例子，考虑这个我之前引用过的声明，解释为什么dropout有效【来自 ImageNet Classification with Deep Convolutional Neural Networks 作者 Alex Krizhevsky, Ilya Sutskever, 和 Geoffrey Hinton (2012)】：“这项技术减少了神经元的相互作用，因为神经元不能依靠其他特定的神经元。因此这就强迫它去学习更鲁棒的特征，这对用许多其他神经元的不同子集配合使用时很有效。”这是一个富有挑衅意味的声明，人们可以围绕这个声明，对其做有成效的研究，指出什么是真，什么是假，需要什么变种和增强。的确，现在有一个研究dropout【和许多变种】的小型的研究行业，试着去理解它是如何做的，它的局限是什么。它和我们讨论的许多其他经验是一样的。每种经验不只是一个（可能）解释，更细致的研究和理解也是一种挑战。

当然，没有时间让任何一个人深入调查所有这些经验性的解释。对于神经网络的研究者社区，会花几十年（或长时间）来开发一个强力的有据可循的理论，告诉我们神经网络是怎样去学习。那就意味着应该拒绝这些经验性的解释，因为它们不严谨且没有充分的证据支撑？不！实事上，我们需要这样的经验来启发和指导我们思考。这就像伟大的探险时代：早期的探险者有时会在错的很离谱的道路上探险（并有新的发现）。之后由于对地理知识的了解，我们纠正了这些错误。当你很难理解某些东西的时候——就像探险家理解地理一样，并且今天我们去理解神经网络——更重要的是去大胆的探索，而不是严格地保证你所想每一步的正确性。因此你应该将这些故事看成是一个对你理解神经网络很有用的指导，同时要正确的认识到这些故事有其局限性，并仔细追踪那些对其有任何帮助的线索。换句话说，我们需要好的故事来激励和启发我们，并严格深入的研究，来揭示问题的本来面目。