关于成本函数所需的两个假设

反向传播全部都是计算网络里成本函数$C$相对于任意权重$w$和偏移量$b$的偏导数$\partial C / \partial w$和$\partial C / \partial b$。为了让反向传播好用，我们需要对成本函数做两个主要假设。在说这些假设之前，还是看一个很有用的关于成本函数的例子。我们将使用上一章（自方程(6)）的二次成本函数。用了上一节的符号，二次成本的形式为

$\begin{eqnarray} C = \frac{1}{2n} \sum_x \|y(x)-a^L(x)\|^2, \tag{26} \end{eqnarray}$

这里：$n$是训练样本的总数量；和是所有训练样本个体$x$；$y = y(x)$是对应的期望输出；$L$表示网络里的层数；还有$a^L = a^L(x)$是当网络的输入是$x$时的激活输出向量。

然后，我们需要关于成本函数$C$什么样的假设，才能让反向传播可以被应用呢？第一个假设是成本函数可以写成一个平均数$C = \frac{1}{n} \sum_x C_x$，对于所有训练样本个体$x$的成本函数$C_x$。这对于二次成本函数来说，单个训练样本的成本是$C_x = \frac{1}{2} \|y-a^L \|^2$。这个假设对本书里所有其他的成本函数都是成立的。

需要这个假设的原因是因为，反向传播实际上让我们计算单个训练样本的偏导数$\partial C_x / \partial w$和$\partial C_x / \partial b$。然后通过计算所有训练样本的平均值恢复成$\partial C / \partial w$和$\partial C / \partial b$。实际上，有了这个假设，我们将假定训练样本$x$已经被确定了，然后去掉$x$下标，将成本$C_x$写成$C$。最终还会将$x$放回去，但就现在而言它是一个让人讨厌的符号，最好还是隐藏掉比较好。

第二个假设是成本函数可以被写成神经网络输出层的函数：

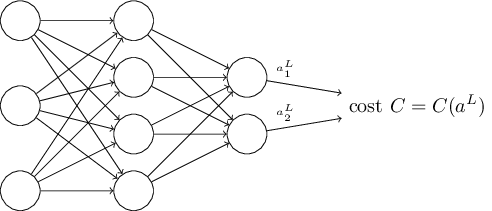
例如，二次成本函数就满足这个需求，因为对于单个训练样本$x$的二次成本可以写成

$\begin{eqnarray} C = \frac{1}{2} \|y-a^L\|^2 = \frac{1}{2} \sum_j (y_j-a^L_j)^2, \tag{27} \end{eqnarray}$

也就是关于输出层激活值的函数。当然，这个成本函数也依赖于期望输出$y$，你可能会疑惑为什么成本函数不是一个关于$y$的函数。记住，尽管这样，但输入的训练样本$x$是固定的，所以输出$y$也是一个固定的参数。实际上，这不是能通过改变权重和偏移量可以实现的，也就是说，这不是神经网络学习的东西。所以就有理由$C$当成是关于输出层激活值$a^L$的函数，$y$仅仅是做为帮助定义此函数的一个参数。