怎样选择神经网络的超参数?
直到现在我也没有解释是怎样挑选如学习率、正则化参数等这些超参数的。我只是提供了一些非常好用的值。实践上,当你要用神经网络来解决一个问题时,找到好的超参数是一件很困难的事情。例如,想象下我们之前提到的MNIST问题,我们正在处理它,但对用什么超参数还是一无所知。假设我们运气很好,第一次尝试就选了和本章之前用的几个超参数一样:30个隐含神经元,小批次的大小为10,训练30代,使用交叉熵成本函数。但我们选的学习率,正则化参数。这是我在一次运行中看到的:
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10])
>>> net.SGD(training_data, 30, 10, 10.0, lmbda = 1000.0,
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 1030 / 10000
Epoch 1 training complete
Accuracy on evaluation data: 990 / 10000
Epoch 2 training complete
Accuracy on evaluation data: 1009 / 10000
...
Epoch 27 training complete
Accuracy on evaluation data: 1009 / 10000
Epoch 28 training complete
Accuracy on evaluation data: 983 / 10000
Epoch 29 training complete
Accuracy on evaluation data: 967 / 10000
我们的分类准确率还不如乱猜来的高!我们的网络简直就是一个随机噪声生成器!
你可以会说,"这好弄,只要把学习率和正则化参数调低下就好"。不幸的是,你不不能预先知道需要作如此的调整。或许真正的问题是30个隐含神经元没有起作用,不管怎样选一个别的超参数会怎么样呢?或许我们至少要100个隐含神经元呢?又或者300个隐含神经元?又或者多个隐含层?又或者用一个不同的方式来对输出进行编码?或许我们的网络在学习者呢,不过需要再训练几代?或许小批次太小了?或者我们需要试试一个不同的权重初始化方式?等等,等等。超参数这块很容易让人摸不着头脑。如果你的网络非常大,或用了大量的训练数据的话,简直会让人崩溃,因为你可能已经训练了几个小时、几天或几周,然而一无所获。如果一直这样的话,会让人失去信心。可能用神经网络来处理你的问题是个错误的方式?或许你该辞掉工作去养蜜蜂?
在本书来说下在神经网络里用来设置超参数的一些经验。目标是帮你开发出一个流程来更好的设置超参数。当然,我不会面面俱道地讲关于超参数的优化。这量个宏大的课题,在任何场景下,它都不是一个被完全解决的问题,在使用正确策略方面,业界也没有形成共识。但还是有些技巧可以提升下网络性能。本节里的经验应该为你开个头。
大概策略:当用神经网络解决一个新问题时,第一个挑战就是让机器学习达到任何重大的突破,就是,网络得出的结果比乱猜要好。这可能非常困难,特别是面对一类新问题的时候。让我们看下如果遇到此类问题的一些对策。
举例来说,假设你是第一次解决MNIST问题。你一开始信心饱满,但当你的第一个网络彻底失败后,你有一点灰心,就像上面的例子那样。接下来做的就是解决掉这个问题。去掉训练和验证图像中,除了0和1的图像。然后试着训练一个区分0和1的网络。这不仅仅是天生比所有10个数字简单,它还减少了近80%训练数据的大小,训练速度提升了5倍。这让我们能更快进行试验,从而更快获取信息来构建一个好的网络。
你可以将你的网络拆成最简单的网络来做有意义的学习,从而进一步加快实验的速度。如果你相信一个[784, 10]的网络来分类MNIST数字,要比乱猜要好,那么就开始用这样的网络试验一下。它要比训练一个[784, 30, 10]的网络快很多,之后你也可以再改回之前的样子。
你可以通过增加监控的频率来对试验做另一种提速。在network2.py中,我们是在每一代训练的结尾监控性能。按每代50,000张图片,这意味着你在看到网络学习效果的反馈前,要等一段时间——在我的笔记本训练[784, 30, 10]的网络,每代差不多要10秒钟。
当然10秒也不是很长的时间,但如果你想尝试挑选几十个超参数的话,就招人烦了,如果你想尝试挑选成百上千个超参数的话,就开始显得致命了。我们可以通过更频繁地监控验证准确率来更快的反馈,比如说,每训练1,000张图片后。此外,替代的使用全部10,000张图片来监控性能,我们可以只用100张验证图片来得到更快的估计。其中最重要的是,网络要能看到足够多的图片来做真正地学习,同时又能对性能做粗略的估计。当然,我们的network2.py程序不是这种类型的监控。但为了演示拼凑出相似的效果,我们将训练数据拆成只有前1,000张MNIST训练图片。让试下看看会发生什么。(为了保持下面的代码简洁,我没有实现只用0和1图片的想法。当然,稍加改动就可以实现。)
>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 1000.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 10 / 100
Epoch 1 training complete
Accuracy on evaluation data: 10 / 100
Epoch 2 training complete
Accuracy on evaluation data: 10 / 100
...
我们得到仍是纯粹的噪声!但有一个很大的改进:我们现在可以在几分之一秒内得到反馈,比大约每10秒一次一次要强多了。这意味着更快地挑选别的超参数进行试验,甚至可以几乎同时尝试多个不同的超参数。
上面的例子中我让,就像之前用的一样。但因为我们改变了训练样本的数量,我们应该改变来保持权重衰减是一样的。这就意味把改成20.0。如果我们这样做的话会出现下面这种情况:
>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 12 / 100
Epoch 1 training complete
Accuracy on evaluation data: 14 / 100
Epoch 2 training complete
Accuracy on evaluation data: 25 / 100
Epoch 3 training complete
Accuracy on evaluation data: 18 / 100
...
哈哈,我们得到了一个信号。尽管不是一个非常好的信号,但仍是一个信号。我们可以在此基础上修改超参数来尝试提升性能。或许我们猜学习率需要再高一点。(你可能会意识到这是一个很蠢的猜测,原因我们稍候再作讨论,请稍加等待。)所以为了测试我们的猜想,我们尝试将调高至:
>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 100.0, lmbda = 20.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 10 / 100
Epoch 1 training complete
Accuracy on evaluation data: 10 / 100
Epoch 2 training complete
Accuracy on evaluation data: 10 / 100
Epoch 3 training complete
Accuracy on evaluation data: 10 / 100
...
好像不太行!它显示我们的猜想是错误的,问题不在于学习率太小。所以我们尝试将换为调低成:
>>> net = network2.Network([784, 10])
>>> net.SGD(training_data[:1000], 30, 10, 1.0, lmbda = 20.0, \
... evaluation_data=validation_data[:100], \
... monitor_evaluation_accuracy=True)
Epoch 0 training complete
Accuracy on evaluation data: 62 / 100
Epoch 1 training complete
Accuracy on evaluation data: 42 / 100
Epoch 2 training complete
Accuracy on evaluation data: 43 / 100
Epoch 3 training complete
Accuracy on evaluation data: 61 / 100
...
这就好多了!因此我们继续去分别调整每一个超参数,逐渐的提升性能。一旦找一个有提升的值,那么就去找一个比较好的值。然后用一个更复杂的架构来做试验,比如说有10个隐含神经元的网络。然后再一次调整和的值。然后增加到20个隐含神经元。随后再调整另外一些超参数。以此类推,在每一个阶段都用留存的验证数据来评估性能,并用这些评估结果来找越来越好的超参数。我们这样做后,由于修改了超参数,通常需要更多的时间才能得到响应,因此我们可以逐步的减小监控的频率。
作为一个大概的策略看上去很有戏。不过,我想回到找超参数的初始阶段,让网络可以学习任何东西。实事上,就算是上面的讨论也未免太乐观了。网络如果一直学不东西的感觉简直让人崩溃。就算你花几天的时间来调整超参数,仍然得不到有意义的反馈。因此我想再强调一下,在早期你应该确保能快速的从试验中得到反馈。直观上讲,这样对问题进行了简化,而架构只会绊住你的脚步。实事上,它提高了效率,因为你更快的找到了对网络有意义的信号。一旦你找到这样的信号,你通常可以通过调整超参数来得到迅速提升。就像许多生活中事物一样,万事开头难。
好,这就是大概策略。现在让我们来看一些设置超参数的一些具体建议。我将集中在学习率和L2正则化参数,还有最小批次大小。然而,许多说法也适应于其他超参数,包括那些与网络结构相关的,别的正则化形式,和一些将在本书后面会遇到的超参数,如动量系数。
学习率:假设我们运行三个MNIST网络,分别用三个不同的学习率,,和。我们把其他超参数设置成之前章节的,跑30代,最小批次大小为10,。我们将回头用全部50,000张训练图片。这是一张展示训练成本行为的图片【图片是用multiple_eta.py生成的】:

用时,直到最后一代成本下降都很平滑。用时,成本开始是下降的,但后面20代接近饱和,随后大部分变化都很小,表现出随机振荡。最后,用时,成本在开始到右侧做剧烈振荡。为了理解振荡的原因,请回想 一下,随机梯度下降算法应该是一步一步地逐渐下降到成本函数的谷底,
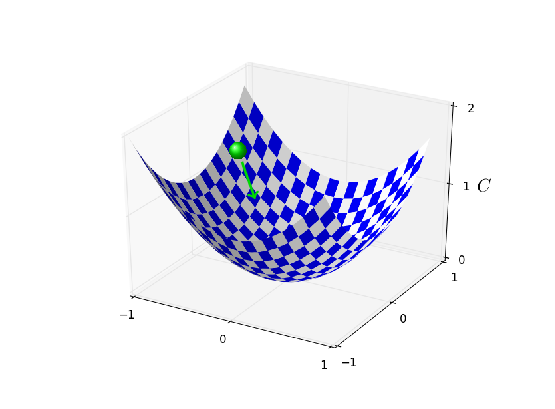
然而,如果太大的话,步伐就会过大,可能会越过最小值,导致算法反而跃上了山峰。f 好像【这幅图是有帮助的,但它的目的是直观的展现将要发生的事性,而不是作为一个完整详尽的解释。简单说下,一个更完整的解决如下:梯度下降对成本函数用了一阶近似,来指导如何减小成本。对于大,成本函数里的高阶项更加重要,并可能会支配其行为,导致梯度下降出现问题。当我们接近极小值和近似极小值时是特别有可能的,因为靠近这样的点,梯度变的很小,就越容易让高阶项来支配其行为。】就是这个导致了当时成本的振荡。当我们选时,开始几步让我们到了成本函数的最小值,只有我们接近最小值时,才会开始遭受过饱和的问题。当我们选用时,在整个前30代根本没有遇到这样的问题。当然,选如此小的引发了另一个问题,即,它减缓了随机梯度下降算法的速度。一个更好的办法是先让,训练20代,然后再切换到。我们将在后面讨论这种可变学习率的调度。但现在让我们继续搞明白如何找一个学习率的好值。
有了这张图片,我们可以按下面这样设置。首先,我们估计下的临界值,在训练数据上成本开始立即下降,而不是振荡或增高。这个估计不用太准确。你可以从开始估计它的量级。如果成本在开始几代就开始下降,那么你应该依次尝试直到你找到一个的值,让成本在开始几代就振荡或增高。对应的,如果当时成本在开始几代就振荡或增高,那么尝试直到你找一个的值让成本在开始几代下降。经过这个过程,将给我们一个对于临界值量级的估计。你可以选择性的改善你的估计,去选出的最大值,让成本在开始几代就下降,比如说或(不需要特别准确)。这给们临界值的一个估计。
显然,的准确值不会比临界值大。实事上,如果的值在超过许多代仍然可用,那么你可能想用一个比较小的值,比方说,临界值的二分之一。这样的选择通常会让你训练很多代,不会引起学习缓慢的问题。
在MNIST数据的场景里,应用这种策略造成对临界值数量级的估计为。在多次改善后,我们得到一个的临界值。按上面的方法,建议用做为学习率的值。实事上,我发现用在30代里表现的都很好,多数情况下,我不担心使用一个较小的值。
这一切看起来都很简单。然而,使用训练数据的成本来挑与我在本节之前说的有矛盾,即,我们挑超参数,应该用留出来的验证数据来评估性能。实事上,我们将用验证数据的准确率来挑正则化的超参数,最小批次大小和网络参数,如层和隐含神经元的数量,等等。为什么与学习率不一样呢?坦白地讲,这是我个喜好的选择,也许有点特殊。原因是别的超参数是在测试集上提升最终的分类准确率,因此在验证数据准确率的基础上选择它们是有意义的。然而,学习率只是偶尔会影响最终的分类准确率。它的真正目的是在梯度下降算法中控制步值的大小,并且监控训练成本是检测步值是否过大最好的方式。说了这么多,都是我个人的喜好。在学习早期,训练成本通常只会随着验证准确率的提升而下降,所以实际上所用的标准不太会造成多大的影响。
使用提前停止来决定训练的代数:正如我们本章早期的讨论,提前停止意味着每一代最后我们应该计算在验证数据上的分类准确率。当这种提升停止时,退出。这种设置代数非常简单。尤其是这意味着我们不用担心要显示的算出代的数量是怎样依赖于别的超参数的。相反,这是自动处理的。此外,提前停止也能自动阻止过拟合。当然这是一个好东西,尽管在试验的早期阶段,最好还是关闭提前停止,这样你可以看到任何过拟合的信号,用它来试验你的正则化方法。
为了实现提前停止,我们说的更清晰一些,什么叫分类准确已经让步提升了。正如我们所见到的,准确类可以在很大范围内跳来跳去,即使是在总体趋势是提升时。如果我们在第一次准确率下降时停止,那么我们将几乎肯定会在有更多提升空间时停止。一个更好的规则是在最好的分类准确率在一段时间内都没有提升时退出。举例来说,假设我们正在做MNIST。那么我们可能会在分类准确率在最近10代都没有提升时终止。这保证我们不会在不走运的训练中停止的太快,但也不会一直等一个永远不会出现的提升。
这个10代内没有提升的规则对于MNIST刚开始的试验是很不错的。然而网络可能会在一个特定的分类准确率上停滞很长一段时间,然后再开始提升。如果你尝试去得到一个真正好的性能,这个10代内没有提升的规则对于停止来说太苛刻了。这种情况下,我建议对于开始的试验用10代内没有提升的规则,再逐渐采用更宽松的规则,为了让你更好地理解网络训练的方式:20代内没有提升,50代内没有提升,以此类推。当然,这引入了一个要优化的新的超参数。然而,实际上,它通常很容易去设置这个超参数来得到好的结果。类似的,对于除了MNIST之外的问题,10代内没有提升的规则可能太严苛,又或不够严苛,这依赖于具体问题。尽管这样,对于一个小试验通常很容易为提前停止找一个很好的策略。
迄今为止我们还没有在我们的MNIST试验中使用提前停止。原因是我们已经在不同的学习方法间做了大量的比较。对于这种比较,每一个场景里最好用相同的代数。然则还是值得修改network2.py来实现提前停止:
问题
修改network2.py来实现代内没有提升策略的提前停止,这里的是一个可以设置的参数。
你能为提前停止想出一个除代内没有提升外的规则吗?理想情况下,这个规则应该在获得高准确率和别训练太长时间这两者间做出妥协。将你的规则加到network2.py中,并跑三个试验,和10代内没有提升比较验证准确率和训练的代数。
学习率规划: 我们一直将学习率当做一个常数。然而改变学习率通常是有益的。在学习过程中的早期,权重很可能很不靠谱。因此最好能用一个大的学习率来让权重变得快一点。之后,我们可以减小学习率,这样我可以对权重作更多的微调。
我们应该怎样去设置学习率规则?有很多方法。一个很自然的方法是用和提前停止一样的基本思想。这个想法是将学习率当作一个常量,直到验证准确率开始变糟了。然后将学习率减小一定的量,比方说二分之一或十分之一。我们重复这样多次,直到,比方说,学习率是初始值的1/1024(或1/1000)。然后我们退出。
一个可变学习规划可以提升性能,但它也为我们打开了一个选择可能学习规划的世界。这些选择可能会让人头疼——你可以花很长时间来优化你的学习规划。对第一个试验我建议还是使用一个常量的学习率。这会让你得到一个好的近似值。之后,如果你想从网络里得到最好的性能,那值得用一个学习规划,沿着之前讲的路线来试验【最近一个演示解决MNIST的学习规划论文是Deep, Big, Simple Neural Nets Excel on Handwritten Digit Recognition 作者 Dan Claudiu Cireșan, Ueli Meier, Luca Maria Gambardella, 和 Jürgen Schmidhuber (2010】。
练习
- 修改network2.py让其实现这样一个学习规划:每当验证准确率萍踪10代内没有提升的规则就减半;并在学习率降到原来的1/128时退出。
正则化参数,: 我建议从一个没有正则化()的初始值开始,并和上面一样测定一个的值。用这个挑选出来的,我们可以用验证数据来为选一个好值。先尝试【我没有一个好的标准来校正这个开始值。如果有人知道一个好的标准,能说明该从哪开始,我是洗耳恭听地(([email protected]))】,然后按10倍的系数,根据需要增加或减小,来在验证数据上提升性能。一旦你找一个好的数量级,你可以调整你的值。做完这些,你应该回去再次优化。
练习
- 使用梯度下降来尝试学习去找像和这样超参数适合值是很诱人的。你能想出一个用梯度下降来的障碍吗?你用想出一个用梯度下降来学习的障碍吗?
本书之前的超参数我是怎么选的:如果你用本节的建议,会发现得到的和的值和本书之前用过的值不太一样。原因是书有写作上的限制,有时去优化超参数不太实际。想想所有不同学习方法间的比较,比如,二次成本函数和交叉熵成本函数间的比较,新老权重初始化方法间的比较,有和没有正则化间的比较,等等。为了让这些比较有意义,我通常会尝试比较的方法间超参数能保持不变(或用适当的方式进行缩放)。当然对所有不同的学习方法,使用一样的超参数来优化是不现实的,所以我所用的超参数作了一些妥协。
如果不妥协的话,我需要去尝试为每一个学习方法去优化那见鬼的超参数。原则上这样可能是一种更好更公平的做法,因为可以看到每一个学习方法最好的结果。然而我们已经沿着这条路做了许多比较,实践上我发现这样计算相当大。这就是为什么我采用对超参数的挑选做了妥协,去使用相对不错(但没有必要是最优的)。
小批次大小:我们怎样来设置小批次大小呢?为了回答这个问题,让我们先假设我们在做在线学习,也就是,用的小批次大小是1。
对在线学习明显的问题就是使用的小批次只有一个训练样本,将导致对梯度的估计误差会比较大。虽然这样,实事上这些误差基本上问题不大。因为单个梯度的估计不需要太准确。我们需要的估计只要能准确到让成本函数趋于保持下降就可以了。它就像你尝试找北极点,但你的指南针不是很靠谱,每次你看它会有10-20度的偏移。假如你经常停来来检查这个指南针,平均下来指南针指的方向应该是正确的,你最后是可以正好找到北极点的。
基于这个说法,听起来我们应该使用在线学习这个方案。实事情况要比这个更加复杂。在上一章的一个问题中我指出,可以用矩阵技术来同时计算一个小批次里所有样本的梯度更新,要比遍历它们好的多。依赖于具体的硬件和线性代数库,计算一个小批次大小(举个例子)为100的梯度估计值,要比分别遍历这个小批次里100个训练样本快很多。可能(比方说)只要50次的时间,而不是100次。
乍一看,这似乎没有什么帮助。用100的小批次大小权重的学习规则像是这样:
这里的和求的是小批次里所有训练样本。与之相对的在线学习的为:
。即使是只做50次的小批次更新,它看起来仍要比在线学习要好,因为我们会频繁的更新。尽管这样,假设在小批次的情况下,我们将学习率放大为原来的100倍,那更新规则变为
这很像用学习率分别做了100次在线学习。但只用了50次单个做在线学习的时间。当然,这和100次在线学习并不完全一样,因为小批次里的都是对一样的权重集做评估的,相对的在线学习的情况下权重的学习是累积的。不过,使用大的小批次很可能会加快学习速度。
考虑到这些因素,挑选最好的小批次大小实际上一种妥协。太小的话,你就不用充分利用好的矩阵库对硬件优化带来的提升。太大就会不能经常更新权重。你挑选的折衷值需要最大化学习速度。所幸挑选让速度最大的小批次大小和其他超参数是相对独立的(除了整体的架构),所以你不用去优化其他超参数来找一个好的小批次大小。因此作法就是对其他超参数用一些接受的就可以(不需要最优),然后尝试一些不同的小批次大小,和上面一样对进行缩放。画出验证准确率与时间(是实际用的时间,而不是每一代的!),并挑一个能性能得到最快提升的小批次大小。用这个选出来的小批次大小,你就可以去着手优化其他超参数了。
当然,正如你所知道的那样,我并没有在我们的网络里做这样的优化。确实,我们的实现变根本没用最快地小批次更新地方式。我几乎所有的例子中都是简单的用了一个10的小批次大小,没有做任何说明和解释。正因为这样,我们可以减小小批次大小来加快学习。我没有这样做,部分是因为想表明小批次大小是大于1的,部分是因为根据我初步的试验这种加速非常有限。尽管这样,在实际实现时,我们肯定会实现最快的小批次更新方式,然后努力的优化小批次大小,来让我们整体的速度最大化。
自动化技术:我已经描述了一些手工优化超参数的经验。手工优化是一个好的了解网络行为的方式。然而不出意料的,在自动化处理上已经出了很多成果。一个常用的技术表格搜索(grid search),它通过超参数空间里的一个表格来做系统搜索。一篇讲表格搜索(主要是容易实现)成就和局限的论文,可以看Random search for hyper-parameter optimization,James Bergstra 和 Yoshua Bengio(2012)。也有很多更复杂的方法被提出来。我不会这里回顾所有这些,但想特别提一篇2012年使用贝叶斯方法来自动优化超参数的论文【Practical Bayesian optimization of machine learning algorithms, 作者Jasper Snoek, Hugo Larochelle, 和 Ryan Adams.】。论文里的代码是对外开放的,已经被其他研究者们成功用了起来。
总结:根据我说过的经验法则,神经网络不会给你最好的结果。但它将给你一个好的开始和未来提升的空间。特别是我已经最大程度上对超参数做了独立的讨论。实践上,超参数间有着联系。你可能用试验,感觉已经差不多了,然后开始去优化,发现它把你优化好的搞的一团槽。实际上,它帮你来回跳动,逐渐靠近合适值。最重要的是,要记住我所描述的建议都是根据经验得来的,并不是一成不变的规则。你应当注意那些没有起作用的迹象,并愿意去尝试。尤其是这意味着要很小心的监控你的网络行为,特别是验证准确率。
实际上加剧挑选超参数难度的是,这门学问被通过许多研究论文和软件程序广泛传播,并且通常只有个别从业者才知道。有许许多多的论文提出(有时互相矛盾)该如何处理的建议。然而鲜有特别有用的论文对这门学文进行总结和提炼。Yoshua Bengio有一篇2012年的论文【Practical recommendations for gradient-based training of deep architectures 作者Yoshua Bengio (2012)】,给出一些用反向传播和梯度下降来训练网络的实际建议,其中包括神经网络。Bengio对许多问题的讨论比我要详细,包括如何更系统的搜索超参数。另一篇很好的论文是一篇1998年Yann LeCun, Léon Bottou, Genevieve Orr 和 Klaus-Robert Müller发表的论文【Efficient BackProp, 作者Yann LeCun, Léon Bottou, Genevieve Orr 和 Klaus-Robert Müller (1998)】。所有这些论文都出现在一本非常有用的2012年的书中,里面收集了许多神经网络中通常用到的技巧【Neural Networks: Tricks of the Trade, 作者 Grégoire Montavon, Geneviève Orr, 和Klaus-Robert Müller】。这本书很贵,但许多文章已经被它们各自的作者发到了网上,一种假说这是出版商的馈赠,你可以用搜索引擎找到它们。
你读这些文章会明白一件事情,尤其是亲自试验后,就是超参数的优化还是一个没有被完全解决的问题。有许多别的技巧可以尝试去提升性能。在作家中有一个说法,就是一本书只有被遗弃了才会有结束。这和神经网络的优化一样:超参数的空间太大了,一个人永远不可能真正完成它的优化,它只是将其遗弃给后面的人。所以你的目标应该是开发一个流程,能让你快速在优化上做出一些不错的成果,同时如果很重要的话,你可以灵活的去尝试更详细地优化。
配置超参数的挑战已经让一些人抱怨,神经网络当和其他机器学习技术相比需要做太多事情了。我听过各种不同的抱怨:“是的,对于这个问题,一个被调好的神经网络可能会得到最好的性能。另一方面,我可以尝试一个随机森林[或SVM或...插入你喜欢的技术],它只要有效就行。我没有时间找出正确的神经网络”。当然,从现实角度出发,使用易于实现的技术是一种好的选择。尤其是你是刚接触这个问题的时候,而且它还没明显的给出机器学习是否能从根本上帮你解决这个问题。另一方面,如果看重是性能上的优化,那么你可能要尝试需要更多专业知识的方法。如果机器学习总是很简单,那就太好了,但没有前车之鉴表明它该是非常简单的。