交叉熵成本函数
大部分人犯错后都会感到很不爽。在开始学习钢琴不久之后,我就开始在观众面前表演了。我非常紧张,开始弹的一个音八度太低。我有点懵,完全无法弹下去,直到有人指出了我的错误。非常尴尬。虽然很不愉快,当我们犯的错误很明确时,我们学习也会很快。你可以打赌,下次我在观众面前表演时一定能演奏出正确的八度!相对的,当我们的错误没有被明确指出来时,我们学习的会慢很多。
理想情况下,我们希望并期待我们的神经网络将从它们的错误中快速的学习。实际中会是这样的吗?为回答这个问题,让我们看一个简单的例子。例子中涉及到的神经元只有一个输入:
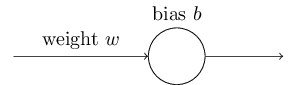
我们让这个神经元学习的东西超级简单:输入为1时输出为0。当然,这是个很简单的任务,我们可以很容易地用手指明一个近似的权重和偏移量,根本不用学习算法。尽管如此,使用梯度下降算法来试图学习一个权重和偏移量会很有启发性。所以让我们来看一下神经元是如何学习的。
为了让事情清晰一些,我将让初始权重为0.6,初始偏移量为0.9。这是作为开始学习的一个通常的选择,我并没有让它们很特别。神经元的初始的输出为0.82,因些在我们的神经元接近期望输出0.0之前,需要相当多的学习才行。点击右下角的"Run"按钮,可以看到神经元是如何学习到输出非常接近0.0的。注意这不是一个事先录好的动画,你的浏览器真真正正的计算了梯度,并使用这个梯度更新了权重和偏移量,再展示出结果。学习率,比较慢,可以让我们能跟踪所发生的事情,但也够快,能让我们在几秒钟内完成最终的学习。成本函数是二次成本函数,,在第一章介绍过。我将帮你想起这个成本函数的确切形式,所以你不用去翻它的定义了。还有你可以再次点那个"Run"按钮来多次查看这个动画。

如你所见,神经元迅速的学习到了一个可以降低成本的权重和偏移量,并给出了一个0.09的输出。这并不是理想中所期望的输出0/0,但已经挺不错的了。尽管如此,假使我们替换开始时的权重和偏移量为2.0。这种情况下的初始输出是0.98,超级差。让我们看下在这种情况下神经元是如何学习到输出为0的。再点一些"Run"按钮:
.png)
尽管这个例子使用的相同的学习率(),我们可以看到开始时的学习要慢很多。的确,在最开始的150代,权重和偏移并没有太大的变化。然后学习开始有效,非常像我们的第一个样例,神经元的输出迅速向0.0靠拢。
这种现象对比人类学习显得很奇怪。就像我本节开始时所说的,我们通常在犯了某些很严重的错误时学习的更快。但我们看到的是我们的人工神经元在严重错误的情况下学习起来很困难——比只有一点错误的时候难得多。而且事实证明,这种现象不仅仅发生在这个简单模型,甚至在更普遍的网络里都会发生。为什么学习会如此缓慢?而我们是否可以找到一种避免变慢的途径?
为了理解这个问题的本质,细想一下我们神经元的学习是通过改变权重和偏移量,它的速率是由成本函数的偏导数决定的,和。所以说“学习很慢”实际上就是说这些偏导数太小。理解为什么它们很小是一项挑战。为了理解它,让我们计算一下这个偏导数。因为我们使用的是二次成本函数,通过公式(6),可以得到
这里的是当训练输入使用时神经元的输出,相应的期望输出为。为了写成更明显的权重和偏移量形式,回想一下,这里的。使用链式法则来区分权重和偏移量,得到
这里替换了和。为了理解这个式子的性质,让我们仔细看下右手边的。回想一下函数的形状:

从图中可以看到当神经元的输出接近1的时候,曲线变得非常平坦,所以变得很小。公式(55)和(56)说明和也很小。这就是学习缓慢的根本原因。此外,我们稍后会看到,在更平常的神经网络里学习缓慢的原因在本质上是相同的,不仅仅是我们一直在用的简单样例。