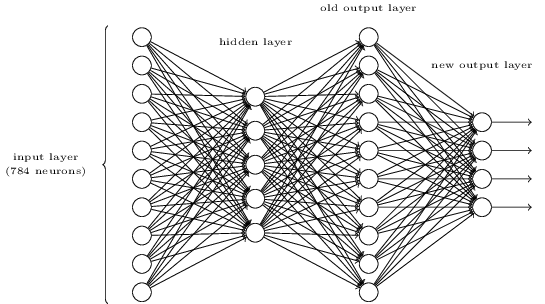
一个简单的手写数字分类网络
定义完了神经网络，让我们回到手写识别上。我们可以将手写识别数字问题拆成两个子问题。首先，我们需要想办法将一个有多个数字的图片分割成一个小图片序列，每个图片包含一个数字。例如我们需要将下面的图片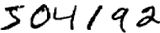
分割成6个小图片
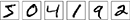，我们人类处理分割问题是非常容易的，但对于电脑程序来说准备分割图片是一项挑战。一旦图片分割后，程序需要对每个数字进行分类。因此对于我们的例子来说 就是让程序将桌面第一个数字
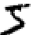识别成5。
我们将集中精力写一个解决第二个问题的程序——对数字进行分类。我们这样做是因为一旦我们有一种好方式来分类数字那么分割问题也不是什么难事。处理分割问题有很多方式。一种方式是尝试很多不同的方式对图片进行分割，然后使用数字分类器对每一个分割样本进行打分。如果数字分类器在所有分片中能确定出其分类，那么它将得到一个高分，如果分类器在一个或多个分片遇到了麻烦那么将得到一个低分。其主要思想是如果分类器遇到了问题，那么很有可能是分割时选得不对。这个方法和其化变种可以很好的解决分类问题。所以与其担心分割问题，还不如集中精力设计一个神经网络去解决更有趣也更困难的问题，也就是识别手写数字。
为了识别数字我们将使用一个三层神经网络：
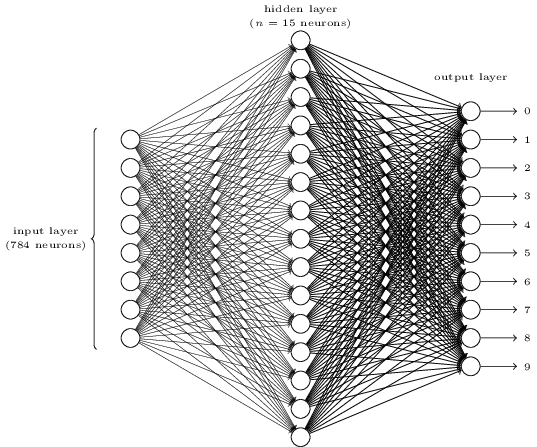
网络的输入层包含着输入像素编码值的神经元。下一节将讨论到，我们的网络的训练数据由许多28x28像素的手写数字扫描图片构成，所以输入层包含了个神经元。简单起见，上面的图示中我省略了一大部分神经元。输入的像素是灰度的，0.0表示的是白色，1.0表示的是黑色，之间的值表示逐渐变暗的灰度。
网络的第二层是隐含层。我们通过使用来表示隐含层中神经元的数目，我们将为尝试不同的值。例子中展示了一个小型隐含层，只有个神经元。
网络的输出层有10个神经元。如果第一个神经元被激活，例如输出是，那么表示网络认为数字是0.如果第二个神经元被激活，表示网络认为数字是1。以此类推。更准确的说法是，我们对输出层的神经元按照从0到1进行了编号，并找出哪一个神经元有最高的激活值。如果这个神经元，比如说，是6号神经元，那么我们的网络将猜测输入的数字是6。对于其他的输出神经元也是这样。
你可能会疑惑为什么我们要用10个输出神经元。毕竟，网络的目标是想告诉我们数字()和输入图像的匹配度。看上去用4个神经元就可以做到，将每个神经元当成二进制的值对待，依赖于神经元的输出是否拉近0或1。4个神经元足够用来编码此问题，因为比10个输入数字的可能值多多了。那为什么我们的网络要用10个神经元呢？终级的解释是经验：我们可以尝试所有的网络设计，然后证明，对于这个实际问题，10个输出神经元的网络要比4个输出神经元识别数字学习的要好。但这仍然留给我们一个疑惑，为什么使用10个神经元的网络更好呢？是否有一些启发方法告诉我们10个输出比4个输出的优势在哪？
为了理解我们为什么这样做，从神经网络的工作原理上理解是有帮助的。首先考虑我们用10个输出神经元这个点。让我们聚焦于第一个输出神经元，它试着判断数字是不是0。这是通过权衡来自隐含层的证据实现的。那些隐含层又做了什么呢？好吧，为了讨论方便，假设隐含层的第一个神经元检测图像是否存在像下面一样的结构：
。
它可以加重输入的像素与图片重叠部分的权重，并减轻其他部分的权重。用相似的方式，让我们为了讨论方便，假设隐含层的第二、三和四个神经元检测是否存在下面的图像：
。
正如你可能已经猜到的那样，这四幅图像合起来组成我们在之前数字展示中0的图像：
。
所以如果隐含层的所有四个隐含层激活，那么我们可以推断出这个数字为0。当然，这不是唯一可以推断图片是0的证据——我们可以用很多其他方式合理的生成一个0（比如说，通过将上面的图像旋转，轻微扭曲）。但看到起来可以保险的说，至少在这个例子里我们可以推断输入是0。
假设神经网络通过这种方式运行，我们可以给出一个貌似合理的解释，为什么10个输出比4个要强。如果我们有4个输出，那么第一个输出神经元需要尝试解决数字对应的最高有效位是什么。而且没有一个简单的方法让最高有效位与上面展示的简单形状相关联。很难想像有什么好的历史原因，让数字的部分形状将与输出里的最高有效位密切相关。
现在来看，上面我们所说都只是一种试探性的说法。没有人说过三层神经网络通过我描述那样通过隐含神经元检测部分简单图形的方式运转。可能一个聪明的学习算法可以找到一些权重分配让我们可以只用4个输出神经元。但作为一种探索性的思考方式，我已经描述过工作得十分理想，并且可以节约你很多时间去设计更好的神经网络结构。
练习
- 有一种方式去决定一个数字的按位的表示方式，通过在上面的三层网络上增加一个额外层。额外层将上一层的输出转换成二进制表示，就像下面图中说明的那样。为新的输出层找出一组权重和偏移。假定第一个三层神经元是这样的，它在第三层（例子中是：old output layer）的正确输出的激活值至少是0.99，错误输出的激活值比0.01小。
