Softmax

这一章我们主要是使用交叉熵成本函数来解决学习缓慢的问题。可我想简短描述另一种处理问题的方法，基于所谓的神经元Softmax层。实际上余下的本章将不会使用softmax层，所以如果你感到很受伤，可以跳过这一节。尽管这样，softmax仍然值得去了解，部分原因是它很有意思，部分原因是我们将在第6章深度神经网络的起讨论中使用它。

softmax的想法是为神经网络定义一个新型的输出层。它和Sigmod层的开始方式一样，都是以$z^L_j = \sum_{k} w^L_{jk} a^{L-1}_k + b^L_j$形式的权重输入【在描述softmax时，会经常使用上一章介绍过的符号。如果你需要重温一下这些符号的含义，你可以再读一下上一章】。然而我们并不用sigmoid函数来输出。作为代替softmax层使用叫做softmax函数来得到$z_j^L$。根据这个函数，第j个输出神经元的激活值$a_j^L$为

$\begin{eqnarray} a^L_j = \frac{e^{z^L_j}}{\sum_k e^{z^L_k}}, \tag{78} \end{eqnarray}$

这里的分母是所有输出神经元的和。

如果你不熟悉softmax函数，公式(78)可能看起来很晦涩。当然啦，没直接说明为什么我们要用这个函数，也看不出能解决学习缓慢的问题。为了更好的理解公式(78)，假设一个有四个输出神经元的网络，对应四个权重输入我们用$z^L_1, z^L_2, z^L_3$和$z^L_4$表示。下面展示的是，调整滑块来展示可能的权重输入值，和对应输出激活值。建议开始时使用最底下的滑块来增大$z^L_4$。

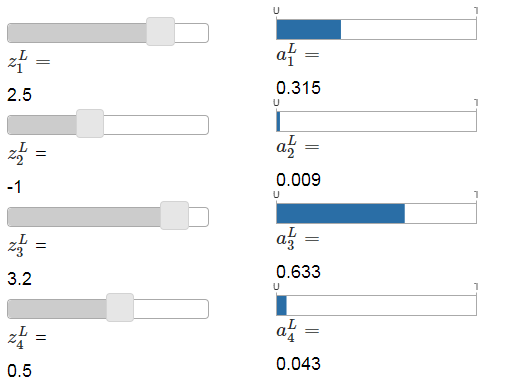
当增大$z^L_4$，你会看到对应的输出激活值$a^L_4$也随之增大，并且其他的输出激活值随之减小。相似的，如果你减小$z^L_4$，那$a^L_4$也减小，其他所有的输出激活值会增大。事实上，如果你仔细观察，会看到其他激活值的变化量总和正好能补偿$a^L_4$的变化量。原因为输出激活值总是保证加起来是1，你可以用公式(78)和一点代数学习来证明：

$\begin{eqnarray} \sum_j a^L_j & = & \frac{\sum_j e^{z^L_j}}{\sum_k e^{z^L_k}} = 1. \tag{79} \end{eqnarray}$

结果就是，如果$a^L_4$增大，那么其他输出激活值就必须减少到一样的总数值，来保证所有激活值的和为1。当然相同的情况也会发生在所有其他激活值上。

公式(78)也暗示输出激活值总是正数，因为指数函数是正数。与上一段观察到的结果想结合，我们可以看到来自softmax层的输出是一组正数，它们的和是1。换言之，来自softmax层的输出可以看作是一个概率分布。

事实上用softmax层来输出概率分布是相当合适的。很多问题可以很方便的将网络输出激活值描述成准确的输出值是$j$的预估概率。所以举例来说，MNIST的分类问题就可以将网络的$a^L_j$描述成，正确的数字分类是$j$的预估概率。

相对的，如果输出层是simoid喜忧参半，我们就不能假定激活值的形式是一个概率分布。这个我就不做证明了，不过显示易见，sigmoid层的激活值形式并不是概率分布的一般形式。因此用sigmoid输出层的问题，就将输出激活值做这样简单的解释（译者注：解释成对应正确结果的概率分布）。

练习

• 构造一个例子展现一个用simoid作为输出层的网络里，输出激活值$a_j^L$的和不会一直为1。

我们开始认识一下softmax函数和softmax层的行为方式。只要回顾一下我们的发现：公式(78)里的指数保证了所有的输出激活值是正数。并且公式(78)的分母里的求和保证了softmax输出的和为1。所以这种特别的形式也就没有那么神秘了：相反，它是保证输出激活值服从概念分布的一种很自然的形式。你可以将softmax当成是对$z^L_j$的缩放，然后把它们并一起形成概率分布。

练习

• softmax的单调性 证明$\partial a^L_j / \partial$在$j=k$时为正，在$j \neq k$时为负。结果就是，增大$z^L_j$一定会增大对应的输出激活值$a^L_j$，并且将减小所有其他输出激活值。我们已经用滑块看到这一现象，但这里需要一个严格的证明。

• softmax的非定域性 sigmoid层的一个优点是输出$a^L_j$是一个对应权重输入的函数，$a^L_j = \sigma(z^L_j)$。解释为什么softmax层不会出现下面的情况：任意特定输出激活值$a^L_j$依赖所有的权重输入。

问题

• 逆向操作softmax层 设想有一个网络用softmax作为输出层，并且其激活值$a^L_j$是已知的。证明其对应的权重输入有着这样的形式$z^L_j = \ln a^L_j + C$，其中常量$C$独立于$j$。

学习缓慢问题： 我们现在已经对softmax层的神经元相当熟了。但我们还没有看到softmax层是怎样解决学习缓慢问题。为了理解这个问题，让我们定义一个对数似然(log-likelihood)的成本函数。使用$x$来表示网络的训练输入，$y$表示对应的期望输出。然后训练输入对应的对数似然成本就是

$\begin{eqnarray} C \equiv -\ln a^L_y. \tag{80} \end{eqnarray}$

举例来说，如果训练MNIST图片集，输入一个图片7，那对数似然成本$-\ln a^L_7$。这看上去看直观，如果网络好用的话，它会确定输入是7。这种情况下它将评估对应的概率值$a^L_7$接近1，而且其成本$-\ln a^L_7$会很小。相反，如果网络做的不好，那概率$a^L_7$会很小，成本$-\ln a^L_7$就会较大。所以对数似然成本的效果很符合我们的预期。

那关于学习缓慢的问题呢？为分析这个问题，回顾一下学习缓慢问题的关键点在于$\partial C / \partial w^L_{jk}$和$\partial C / \partial b^L_j$量的状况。我不会直接给出推导过程，这将是你们要做的一道题，下面用一点代数就可以证明【注意这里我滥用了符号，其中的$y$和上一段的使用方式有所不同。在上一段$y$是表示网络的期望输出——也就是，如果输入的是"7"的图片，结果应该是7。但在公式中，$y$表示对应7输出激活值的向量，也就是向量中的值都是0，除了第7个位置】

$\begin{eqnarray} \frac{\partial C}{\partial b^L_j} & = & a^L_j-y_j \tag{81}\\ \frac{\partial C}{\partial w^L_{jk}} & = & a^{L-1}_k (a^L_j-y_j) \tag{82} \end{eqnarray}$

这些公式和我们之前分析交叉熵时候得到的表达式很类似。例如，比较一下公式(82)和(67)。它们是相同的公式，虽然后者求的是所有训练实例的平均值。并且，就像之前的分析，这些公式能保证我们不会遇到学习缓慢的问题。事实上，softmax输出层用对数似然成本函数，就像sigmoid输出层用交叉熵成本函数一样，是非常合适的。

鉴于这种相似性，是否可用在sigmoid输出层里用交叉熵，或softmax输出层里用对数似然呢？事实上，在很多场景下它们都表现的很好。余下的本章会使用sigmoid输出层和交叉熵成本函数。后面在第6章里，我们有时会用softmax输出层和对数似然成本函数。替换的原因是让我们后面的网络能和权威论文中网络更相近。作为一条更普遍的原则，softmax加对数似然非常适合将输出激活值当成概率的场景。这不是总是受人重视，但在涉及不相关类的分类问题（如MNIST）时很有用。

问题

• 推导出公式(81)和(82)

• 为什么要叫"softmax"？ 假设我们将softmax函数改成下面的样子

$\begin{eqnarray} a^L_j = \frac{e^{c z^L_j}}{\sum_k e^{c z^L_k}}, \tag{83} \end{eqnarray}$

其中$c$是一个正常数。注意$c = 1$对应的是就是标准的softmax函数。但如果$c$用不同的值就是一个不同的函数，但还是保持与softmax相似的性质。尤其是输出激活值和平常的softmax一样是服从概率分布的形式。假设让$c$变得很大，比如$c \rightarrow \infty$。那输出激活值$a^L_j$的极限值是多少？在解决这个问题后，你就会明白为什么说$c=1$时的函数是最大值下函数的"软化"版本了。这就是"softmax"术语的最初形式。

• 用softmax和对数似然成本函数做反向传播 上一章我们推导了包含sigmoid层网络的反向传播算法。为了将这个算法应用到softmax层的网络里，我们需要算出最终层里误差的表达式$\delta^L_j \equiv \partial C / \partial z^L_j$。证明其正确的表达式为：

$\begin{eqnarray} \delta^L_j = a^L_j -y_j. \tag{84} \end{eqnarray}$

这个表达式可以让我们对使用softmax和对数似然成本函数的网络使用反向传播算法。