Sigmoid神经元

学习算法听起来很棒。但是我们怎么才能为一个神经网络设计一个这样的算法呢？假设我们有一个感知机网络，想通过使用学习去解决一些问题。例如，网络的输入可能是一张手写数字扫描图片的原始像素数据。我们想让网络通过学习权重和偏差来输出正确的数字分类。为了看到学习是怎样工作的，假设我们在一些权重（或偏差）上做了一点小小的改动。我们想的是这点小改动会引起网络输出发现一点相应的小改变。我们会看到，这个性质可以让学习变得可能。按计划下面就是我们所想的（显然对于手写识别来说这个网络有点太简单了！）：

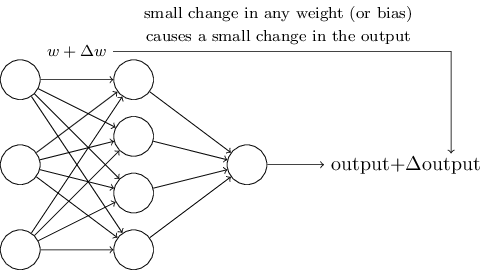
如果我们可以实现权重（或者偏差）的小改变只会让输出出现小改变，那么我们利用这点去修改权重和偏差来让神经网络做一些我们想要的行为。例如，假设神经网络将一个"9"的图片错误的分类成"8"了。我们可以计算出在权重和偏差上作多小的改动可以让神经网络对图片的分类更接近"9"。然后我们重复这样做，不断的改变权重和偏差得到越来越好的输出。这样神经网络就可以学习了。

问题是当神经网络里有感知机的时候并不是像上面那样处理的。实际上，神经网络里一个感知机的权重和偏差的小小改变，有时会引起感知机输出的完全反转，例如从0到1。这种反转可能会引起剩下网络的行为变得非常复杂。所以现在"9"可能分类是正确的，但其他图片可能在神经网络里将变得难以控制。这就造成很难发现逐渐改变神经网络的权重和偏差，神经网络会慢慢接近我们想要的行为。也许有一些聪明的方法去解决这个问题。但现在还不是揭示感知机网络如何学习的时候。

我们可以通过介绍一种新的叫做Sigmoid神经元的人工神经元来解决这个问题。Sigmoid神经元和感知机很相似，但变得可以让对权重和偏差的小小改动只会引起输出的小改变。这是让Sigmoid神经元网络能够学习的关键因素。

好的，让我们来描述一下Sigmoid神经元。我们将使用和描述感知机一样的方式来描述Sigmoid神经元：

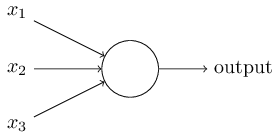
就像感知机一样，Sigmoid神经元有输入，$x_1, x_2,\ldots$。但不只是0或1，这些输入可以是0到1之间的任何值。例如，$0.638\ldots$对Sigmoid神经元来说是一个正确的值。和感知机一样，Sigmoid神经元也有针对个输入的权重，$w_1, w_2,\ldots$，和一个总体的偏差$b$。但是不再是0或1，而是$\sigma(w \cdot x+b)$，这里的$\sigma$叫做Sigmoid函数(旁注：顺便说一下，$\sigma$有时被叫做逻辑函数，这种新类型神经元叫做逻辑神经元。由于这个术语被诸许多神经网络工作者使用，所以记住这个它还是有好处的。虽然我们将一直使用Sigmoid这个术语。)，被定义为：

$\begin{eqnarray} \sigma(z) \equiv \frac{1}{1+e^{-z}} \tag{3} \end{eqnarray}$

展示的再明确一点的话，输入为$x_1, x_2,\ldots$，权重是$w_1, w_2,\ldots$，并且偏差是$b$的Sigmoid函数的输出是：

$\begin{eqnarray} \frac{1}{1+\exp(-\sum_j w_j x_j-b)} \tag{4} \end{eqnarray}$

第一眼看上去Sigmoid神经元跟感知机很不同。如果你对Sigmoid函数的代数形式不是很熟悉的话，它可能看起来很晦涩难懂。实际上感知机和Sigmoid神经元之间有很多相似之处，并且Sigmoid函数的代数形式比起一个真正的门槛来说提供了更多的技术细节让我们去理解。

为了理解与感知机模型的相似之处，假设$z \equiv w \cdot x + b$是一个大正数，那么$e^{-z} \approx 0$所以$\sigma(z) \approx 1$。也就是说，当$z = w \cdot x+b$是一个大正数时，Sigmoid神经元的输出是接近$1$的，就像感知机一样。假设另一面$z = w \cdot x+b$是一个极负的数，那么$e^{-z} \rightarrow \infty$,并且$\sigma(z) \approx 0$。所以当$z = w \cdot x+b$是极负的数时，Sigmoid神经元的行为跟感知机很相似。只有当$w \cdot x+b$在合适大小的时候，跟感知机模型有较大不同。

那关于$\sigma$的代数形式呢？我们该如何理解？实际上，$\sigma$的具体形式并不重要，真正需要关心的是函数所绘的形状。下面是其形状：

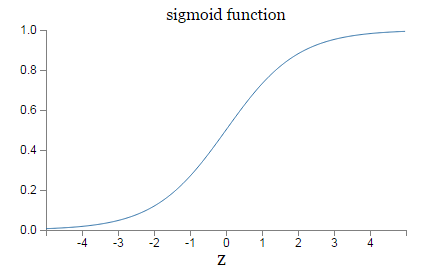
这个形状是一个平滑版本的阶梯函数：

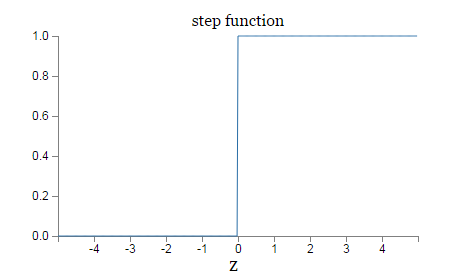
如果$\sigma$实际上是一个阶梯函数，那么Sigmoid神经元就是一个感知机，因为输出将根据$w\cdot x+b$是正是负而输出1或0（旁注：实际上，当$w\cdot x+b = 0$时感知机输出0，然而阶梯函数输出1.所以严格来讲我们需要修改阶梯函数的这个点。但是你理解意思就好。）。通过使用真实的$\sigma$函数，其实已经隐含在上面了，一个平滑的感知机。的确，$\sigma$函数的平滑程度是一个重要的性质，不是具体的形式。$\sigma$函数的平滑程度意味着，权重的微小改变$\Delta w_j$和偏差的$\Delta b$将让神经元的输出产生微小改变$\Delta \mbox{output}$。实际上，计算得出$\Delta \mbox{output}$是非常近似于

$\begin{eqnarray} \Delta \mbox{output} \approx \sum_j \frac{\partial \, \mbox{output}}{\partial w_j} \Delta w_j + \frac{\partial \, \mbox{output}}{\partial b} \Delta b, \tag{5} \end{eqnarray}$

是所有权重$w_j$的和，其中$\partial \, \mbox{output} / \partial w_j$和$\partial \, \mbox{output} /\partial b$分别表示$\mbox{output}$关于$w_j$和$b$的偏导数。如果你对偏导数不是很熟悉也不要担心！虽然上面的表达式看上去很复杂，全都是偏导数，实际上说了一件很简单的事情（同时也是非常好的消息）：$\Delta \mbox{output}$是一个关于权重和偏差变化$\Delta w_j$$\Delta b$的线性函数。线性可以让我们很简单的选择权重和偏差的微小改变达到任意我们预期关于输出的微小改变。所以虽然Sigmoid神经元有很多和感知机相似的性质，但这让其更容易能计算出关于权重和偏差变化多大将改变输出。

如果$\sigma$真正有意义的是形状而不是具体形式，那为什么要用公式(3)这个特定形式呢？实际上书的后面将偶尔考虑对输出是$f(w \cdot x + b)$的神经元使用一些其他的激活函数$f(\cdot)$。当使用不同的激活函数后主要的变化是公式(5)里的偏导数的值将发现变化。事实证明后面当我们计算这些偏导数的时候，使用$\sigma$函数将简化代数计算，简单是因为指数在求微分时有十分可爱的属性（译者注：$e^x$的微分还是其自身）。总之，$\sigma$函数在神经网络中被广泛使用，并且它的激活函数在本书中也将经常使用。

我们怎样解释Sigmoid神经元的输出呢？显然Sigmoid神经元和感知机有很大的不同，它不是只输出0或1，可以是0到1之间的任意实数，比如$0.173...$和$0.689...$都是合法的输出。这很有用，例如，如果我们可以用输出表达图片像素点的平均灰度输入到神经网络。但有时这会很麻烦。假设我们想让神经网络的输出表达要么"输入的图像是9"，要么"输入的图像不是9"。显然，作为感知机可以通过输出0或1轻松办到。但实际上我们可以使用一个约定来处理这个问题，比如，决定让所有大于等于$0.5$的输出表示"是9"，而所有小于$0.5$的输出表示"不是9"。我将在使用这样的约定时给出明显说明，所以这将不会引起误会。

练习

• Sigmoid神经元模拟感知机，第一部分

假设我们让感知机网络里所有的权重和偏差，乘以一个正常数$c > 0$。证明网络的行为不会有任何改变。

• Sigmoid神经元模拟感知机，第二部分

假设我们有一个和上题一样的感知机网络。假设感知机网络的输入已经被选好。我们不需要实际值，只需要保证输入是固定的。假设权重和偏差对网络里所有特定感知器的输入$x$都满足$w \cdot x + b \neq 0$。现在将网络里所有感知器替换成Sigmoid神经元，并将权重和偏差乘以一个正常数$c > 0$。证明在$c \rightarrow \infty$极限里，Sigmoid神经元网络和感知机网络是一样的。但为什么当有一个感知器$w \cdot x + b = 0$为0时会不满足呢？