正则化

增加训练数据的数量是一个减少过拟合的方式。有别的方式可以减少过拟合的发生吗？一种可行的办法是减小网络的大小。尽管这样，大型网络比小型网络更有强大的潜力，所以这个只是我们勉强能接受的选择。

幸运的是，有别的技术可以减少过拟合，即使在网络固定，训练数据固定的情况下。它们被称为正则化(regulariztion)技术。这一节介绍其中一个最常用的正则化技术，这个技术有时被称为权重衰减（weight decay）或L2正则化。L2正则化的思想是在成本函数上加一个额外的项，这个项叫做正则项(regularization term)。这里是正则化的交叉熵：

$\begin{eqnarray} C = -\frac{1}{n} \sum_{xj} \left[ y_j \ln a^L_j+(1-y_j) \ln (1-a^L_j)\right] + \frac{\lambda}{2n} \sum_w w^2. \tag{85} \end{eqnarray}$

第一项只是普通的交叉熵表达式。但我们加了第二项，即网络所有权重的平方和。通过一个$\lambda / 2n$因子进行缩放，这里$\lambda > 0$被称为正则划参数，$n$和往常一样，表达训练集的大小。后面将讨论如果挑选$\lambda$。同样值得注意的是正则项里没有包含偏移量。下面将回头再说这个。

当然，也可以正则化其他成本函数，如二次成本函数。用很类似的方式：

$\begin{eqnarray} C = \frac{1}{2n} \sum_x \|y-a^L\|^2 + \frac{\lambda}{2n} \sum_w w^2. \tag{86} \end{eqnarray}$

在所有情况下正则化成本函数可以写成

$\begin{eqnarray} C = C_0 + \frac{\lambda}{2n} \sum_w w^2, \tag{87} \end{eqnarray}$

这里的$C_0$是原始的非正则化成本函数。

直观上讲，正则化的作用是让网络更喜欢学习更小的权重，其他不变。大的权重只有在对第一部分的成本函数提升很大的情况下才允许出现。换句话说，正则化可以看成是一种在寻找小权重和最小化原始成本函数之间的一种折衷方式。折衷两者的相对重要性取决于$\lambda$的值：$\lambda$越小则更趋向于最小化原始成本函数，相反$\lambda$越大则更趋向于小的权重。

现在确实很难看出，为什么这种折衷能帮助减少过拟合！但事实证明它确实可以。我们将在下一节解决为什么它会有帮助这个问题。但首先，让我们通过一个例子来展示正则化确实减少了过拟合。

为了构建这样一个例子，首先需要知道在正则化的网络里如何使用随机梯度下降学习算法。其他是需要知道如何对网络里所有的权重和偏移量计算偏导数$\partial C / \partial w$和$\partial C / \partial b$。取公式(87)的偏导数给出

$\begin{eqnarray} \frac{\partial C}{\partial w} & = & \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w \tag{88}\\ \frac{\partial C}{\partial b} & = & \frac{\partial C_0}{\partial b}. \tag{89} \end{eqnarray}$

其中$\partial C_0 / \partial w$和$\partial C_0 / \partial b$项可以使用上一章说的反向传播来计算。因此我们可以看到很容易就可以计算出正则成本函数的梯度：只要和通常一样使用反向传播，然后在所有权重项的偏导数上加上$\frac{\lambda}{n} w$。对于偏移量的偏导数没有变化，因此对于偏移量的梯度下降学习规则和通常的一样：

$\begin{eqnarray} b & \rightarrow & b -\eta \frac{\partial C_0}{\partial b}. \tag{90} \end{eqnarray}$

对于权重的学习规则变为：

$\begin{eqnarray} w & \rightarrow & w-\eta \frac{\partial C_0}{\partial w}-\frac{\eta \lambda}{n} w \tag{91}\\ & = & \left(1-\frac{\eta \lambda}{n}\right) w -\eta \frac{\partial C_0}{\partial w}. \tag{92} \end{eqnarray}$

这和通常的梯度下降学习规则基本上一样，除了第一个权重$w$使用因子$1-\frac{\eta \lambda}{n}$调整了比例。这种比例调整有时被称为权重衰减(weight decay)，因为它让权重变小了。乍一看这似乎让权重无限趋向于0。但这不会发生，因为如果在非正则化的成本函数里出现了这样衰减，其他项会引导权重增加。

好了，这就是梯度下降的工作方式。那随机梯度下降呢？就行在非正则化的随机梯度下降一样，可以通过对一个小批次的m个训练样本求平均值来估计$\partial C_0 / \partial w$。从而正则化学习规则的随机梯度下降变为(转自公式(20))

$\begin{eqnarray} w \rightarrow \left(1-\frac{\eta \lambda}{n}\right) w -\frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial w}, \tag{93} \end{eqnarray}$

这里的和求的是小批次里所有训练样本$x$，$C_x$是每个训练样本的(非正则化)成本。这和通常的随机梯度下降学习规则一样，除了$1-\frac{\eta \lambda}{n}$权重衰减因子。最后，为了完整，来看下偏移量的正则化学习规则。当然和非正则化的情况是完全一样的(转自公式(21))

$\begin{eqnarray} b \rightarrow b - \frac{\eta}{m} \sum_x \frac{\partial C_x}{\partial b}, \tag{94} \end{eqnarray}$

这里的和求的是小批次里所有训练样本$x$。

让我们来看一下正则化是怎么改变我们神经网络性能的。我们将用一个有30个隐藏神经元、小批次大小为10，学习率为0.5，使用交叉熵成本函数的网络。这次我们使用$\lambda = 0.1$的正则化参数。注意在代码里使用的变量名为lmbda，因为lambda是Python里的保留字，没有相关意义。还是再一次用test_data而不是validation_data。严格地讲，根据之前讨论过的原因，应该用validation_data的。但为了能让结果和之前非正则化的结果有更直接的比较，决定还是用test_data。你可以很容易的把代码改为换用validation_data，然后你会发现结果是相似的。

>>> import mnist_loader 
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper() 
>>> import network2 
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data[:1000], 400, 10, 0.5,
... evaluation_data=test_data, lmbda = 0.1,
... monitor_evaluation_cost=True, monitor_evaluation_accuracy=True,
... monitor_training_cost=True, monitor_training_accuracy=True)

训练数据上的成本与之前非正则化的场景比，一直都是下降的【这张和下面二张图是用代码overfitting.py生成的】：

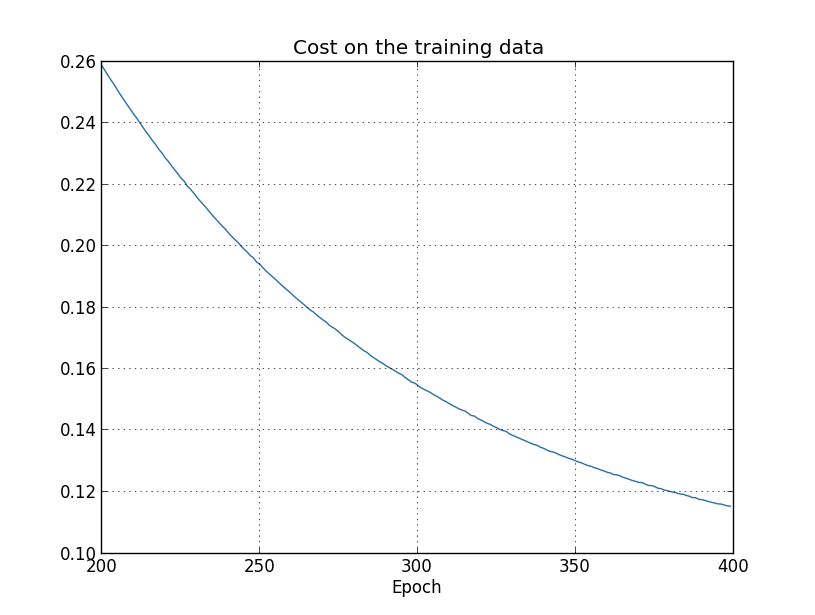
但这次test_data上的准确率在整个400代里是持续递增的：

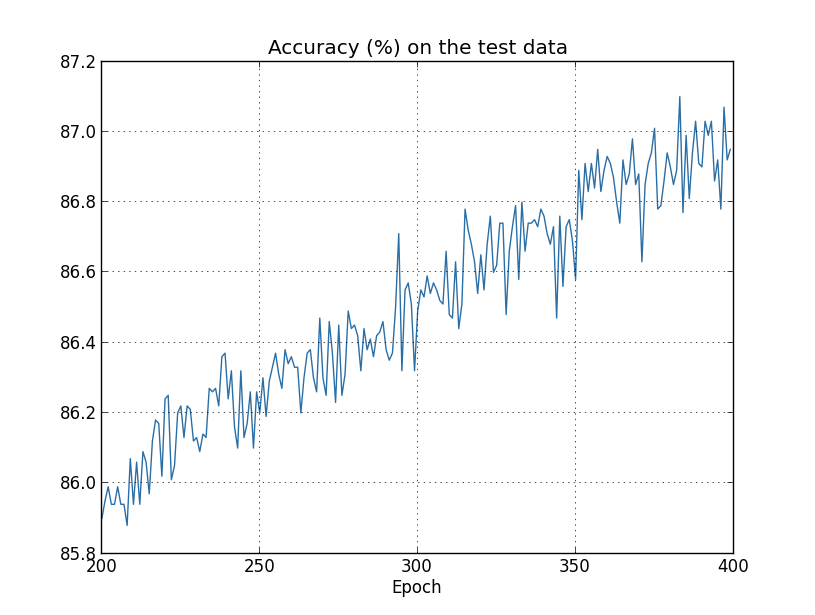
很明显，正则化的使用抑制了过拟合。而且，准确率要高的多，其分类准确率的峰值由之前非正则化下的82.27%提高到了87.1%。实事上，应该继续训练原来的400代几乎肯定可以得到更好的结果。根据经验，正则化看上去可以让我们的网络泛化的更好，并显著减少过拟合的影响。

如果我们离开人为设定的只有1,000训练图片的环境，回到用所有50,000张图片的训练集呢？当然，我们已经看到在所有50,000张图片的情况下，过拟合问题已经减少很多了。正则化能进一步提升吗？让我们保持超参数和之前的一样——30代，学习率0.5，小批次大小为10。尽管这样，我们需要修改一下正则化参数。因为训练集的大小$n$由$n = 1000$改成了$n = 50,000$，这会影响权重衰减因子$1 - \frac{\eta \lambda}{n}$。如果我们继续用$\lambda = 0.1$将意味权重衰减变小，这会导致正则化的效果减弱。我们将其改为$\lambda = 5.0$来补偿。

好，让我们来训练网络，不过要先停下重新初始化权重：

>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5,
... evaluation_data=test_data, lmbda = 5.0,
... monitor_evaluation_accuracy=True, monitor_training_accuracy=True)

得到的结果为：

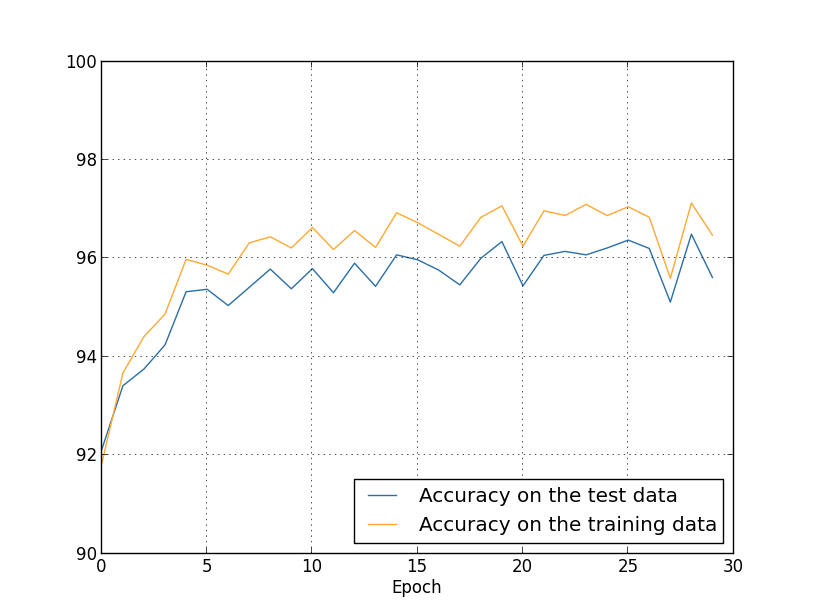
这里有很多好的消息。首先，我们在测试数据上的分类准确类由未正则化时的95.49%提升到了96.49%。这是一个很大的提升。其次，我们可以看到训练和测试数据上结果的差距相比之前要小很多，基本上在1%以下。这仍是一个很大的差距，但我们明显能看到在减少过拟合方面取得了本质上的进展。

最后，我们来看一下当用100个隐藏神经元和$\lambda = 5.0$的正则化参数时测试准确率会是多少。我不会在这里分析过拟合的细节，只是单纯为了好玩，看下用了交叉熵成本函数和L2正则化这些新技巧后准确率会有多高。

>>> net = network2.Network([784, 100, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.5, lmbda=5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True)

最终的结果是在验证数据上的分类准确率为97.92%。与30个隐藏神经元的情况相比这是一个很大的进步。实事上，只要再调整一点，在$\eta = 0.1$和$\lambda = 5.0$的参数下跑60代就可以破98%大关，在验证数据上大致98.04%的分类准确率。对于152行的代码来说，这是一个不坏的结果。

我已经描述了正则化可以减少过拟合并提高分类准确率。实事上，还有其他益处。根据经验，当然用不同（随机）的初始权重多次跑我们的MNIST网络时，我发现非正则化偶尔为被“卡住”，显然是掉进了成本函数的局部最小值。结果就是不同的运行给出的结果差别相当大。相反，正则化的运行给出更多简单重复的结果。

为什么会这样？如果成本函数没有正则化，那么在其他方面都相同的情况下，权重向量的长度更倾向于变长。随着时间的推移，这确实会让权重向量变得非常大。这将导致权重向量会卡在大致相同的方向上，因为当权重长度很长时，改变引起的梯度下降只能很微小的影响方向。我相信这种现象让我们的学习算法很难搜索权重空间，从而很难找到成本函数的最小值。