为什么正则化可以减少过拟合?
我们已经看到了正则化对减少过拟合是有帮助的。这是令人鼓舞的,但不幸的是,并没有明显给出为什么正则化会有帮助!人们用一个标准的故事来解释接下来发生的事情:从某种意义上讲,小权重意味着更小的复杂度,所以能对数据提供简单和更有力的解释,因此应该被优先考虑。这是一个非常简洁的故事,不过包含了一些看上去有些可疑或让人困惑的元素。让我们将这个故事分解并严谨的检查一下。要这样做的话,让我们假设有一个简单的数据集来生成我们想要的模型:
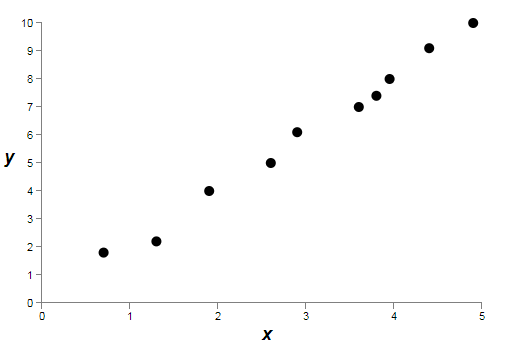
这里我们在潜在地学习一些现实世界中的现象,其中和表示现实世界中的数据。我们的目标是构建一个关于的函数模型,来预测。我们应该尝试使用神经网络来构造这样的模型,但我要做更简单的事情:我将尝试把作为的一个多项式。我这样做而不是用神经网络是因为,使用多项式将让事情变得特别清晰。一旦我们理解多项式的情况,我们会转到神经网络上。现在,在上面的图片里有10个点,意味着我们可以找到一个唯一的9阶多项式来精确地匹配数据。这里是多项式的图片【我不会展示明确的系数,尽管它们可以很容易的用诸如Numpy的polyfit程序找到。如果你好奇的话,你可以在图片的代码里看到多项式的准确形式。它从生成图片代码的14行开始,命名为p(x)的函数。】:
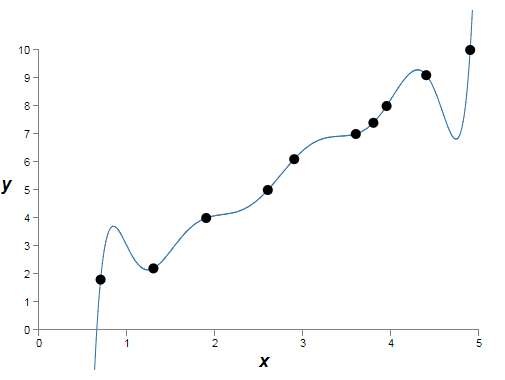
这匹配的很精确。但我们也可以用线性模型来得到一个好一些的匹配:
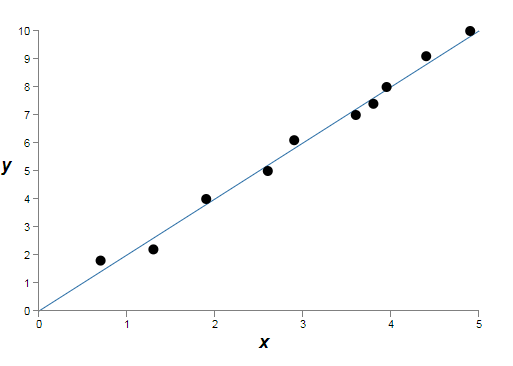
它们中的哪一个模型更好?哪一个更真实?哪一个能更好的泛化到相同的潜在真实世界现实的样本呢?
这些问题很难回答。实事上,没有更多关于潜在真实世界现象的信息,我们是不能判断上面任意问题的确切答案。但让我们来考虑两个可能:(1)其实,9阶多项式是真实描述真实世界现象的的模型,因此这个模型将会完美地泛化;(2)正确的模型是,但由于测量误差,产生了一点额外的噪声,所以模型没有准确匹配。
没有一个先验可能性来说这两个可能是正确的。(或者,如果有第三个可能也是如此)。讲道理理它们中的一个应该是正确的。并且它们差别不小。这两个模型在提供的数据上相差不大。但假设我们想预测一些值比较大,比图上任何一个值都大很多的对应的。如果这样做的话两个模型的预测将天差地别,其中9阶多项式模型的输出将由项主导,然而线性模型仍是线性的。
科学界一个观点是说我们应该趋向于更简单的解释,除非刻意不这样做。当我们找一个简单的模型看上去能解释大量数据,我们会不由的喊出“有了!”毕竟,一个简单的解释不太可能仅仅是巧合。我们宁愿猜测这个模型一定表达出了现象中一些潜在的事实。在手头上的这个例子,模型看上去要比简单的多,如果这种简单是偶然发生,我们会感到惊讶,所以我们猜想表达出了一些潜在的事实。从这一点上看,9阶模型真正学习到的只是局部噪声的效果。因此当9阶模型对特定数据点拟合的好,那这个模型将不能泛化到其他数据点,而噪音线性模型将具体有更强的预测能力。
让我们看看这个观点对神经网络意味着什么。假设我们的网络通常权重较小,在正则化的网络里常是这样。小的权重意味着如果我们在这和那对输入作一些随机改变,网络的行为不会有太大变化。这就让正则化的神经网络很难从数据中学习到局部噪声的效果。把它当成是一种让单个证据对网络输出影响很小的方法。相反,正则化网络的学习只对各种证据中经常在训练数据中出现的才会有响应。相比之下,一个权重很大的网络在响应输入的较小改变时,行为会发生很大变化。因此未正则化的网络会用大量的权重学习到一个复杂的模型,携带了大量训练数据中的噪声信息。简言之,正则化网络被限制来基于训练数据里经常出现的模型来构造相对简单的模型,并抑制学习训练数据中噪声的特征。我们希望这会驱使网络对手边的现象做真正的学习,并从学到的东西中得到很好的泛化能力。
按那样的说法,趋向于更简单解释的想法可能会让你感到不安。人们有时把这种想法称为“奥卡姆剃刀”,并积极的应用,就好像它有常规科学原理的地位一样。但,它当然不是一种常规科学原理。没有一个逻辑上的推理证明简单的解释比复杂的解释更好。实事上,有时相对复杂的解释才是正确的。
让我们看两个更复杂解释才是正确的例子。在20世纪40年代物理学家Marcel Schein宣布发现了一种新的自然粒子。他工作的公司,通用电器,欣喜若狂,广泛的宣传了这个发现。但物理学家Hans Bethe表示怀疑。Bethe拜访了Schein,并查看显示有Schein新粒子轨迹的底片。Schein给Bethe一张张的展示了底片,但每一张底片Bethe都指出了一些问题,并建议应该弃用这些数据。最后,Schein给Bethe展示了一张看上去不错的底片。Bethe说它可能只是统计学习上巧合。Schein:“是的,但即使用你的公式来统计也是1/5的概率”。Bethe:“但我们已经看过5张底片了”。最后Schein说:“但在我看来,每一张底片都是好的,每一张图片也是好的,你用不同的理论来解释,然而我有一个假设可以解释所有底片,那就是它们是[新粒子]”。Bethe回复道:“你与我解释的根本不同在于,你的是错的,而我的所有解释都是对的”。后来经过确认,Bethe是对的,Schein的粒子是不存在的。【这个故事是物理学家Richard Feynman在一次与历史学家Charles Weiner的一次采访中讲的】
第二个例子是在1859年,天文学家Urbain Le Verrier观察到水星轨道的形状与牛顿的万有引力理论说的有些许差异。与牛顿的理论只有很小的偏差,当时好几种解释都说牛顿的理论是基本正确的,但需要一点修改。1916年,爱因斯坦展示了这个偏差可以用他的广义相对论很好的解释,他的理论上与牛顿万有引力理论完全不同,而且是基于非常复杂的数学运算。尽管更加复杂,今天我们都已经接受了爱因斯坦的解释是正确的,而牛顿万有引力,即使是其修改形式,也是错误的。这只是一部分,因为我们现在知道爱因斯坦的理论可以解释许多牛顿理论难以解释的现象。此外,更神奇的是,爱因斯坦的理论准确的预测了许多牛顿万有引力根本无法预测的现象。但这些神奇的物质在早些时候还不能完全的显示出来。如果只是基于简单性来做判断的话,那么某些牛顿理论的修改形式也许会更加吸引人。
从这些故事中我们可以吸取三个经验教训。第一,判断两个解释哪一个更“简单”是一件很微妙的事情。第二,即使我们可以做出这样的判断,也要很小心地使用简单性原则!第三,一个模型的真正考验不是简单,而是它在预测新现象,新环境下的行为表现如何。
话虽如此,但仍需谨慎对待,经验上讲正则化的神经网络通常要比非正则化网络泛化能力更强。因此本书余下章节会经常使用正则化。上面讲述的三个故事只是想表达为什么没有人能开发出一套完整的理论体系来解释为什么正则化能提升网络的泛化能力。确实研究者们在不断的写一些论文来尝试不同的正则化方法,对它们进行比较,看看哪些效果更好,并试图理解为什么不同的方法的效果好或不好。因此你可以把正则化看成是凑合出来的东西。当然它通常是有用的,我们没有一个整体上让人满意的系统来理解为什么会这样,仅仅是凭不完善的启发方法和经验法则。
这有一堆深层次的问题,触及到了这项科学研究的核心。问题的本身就是我们怎样去泛化。正则化可能给我一些计算技巧让我们的网络能泛化的更好,但它并不能帮我们去理解泛化的本质,或者什么是更好的方法。【这些问题追溯到了归纳问题,著名的讨论是英格兰哲学家 David Hume的An Enquiry Concerning Human Understanding(1748)。归纳问题已经在David Wolpert和 William Macready的没有免费午餐理论(链接)(1997)给出了现代机器学习方式。】
这就很尴尬,因为在日常生活中,我们人类能很好的对现象进行泛化。只要给一个幼儿少量大象的图片,就能很快学会去识别别的大象。当然,他们偶尔犯一些错误,也许会将犀牛混淆成大象,但总体上这个过程的准确率是很高的。因此我们有一个系统——人类的大脑——有大量的自由参数。在看了一张或少量几张训练图片后,这个系统学习去泛化到别的图片。我们的大脑在某些场景下,正则化出奇的好!我们是怎样做到的呢?这一点我们还不是很清楚。期望能在几年内能在人工神经网络方面开发出更有力的正则化技术,能从根本上让神经网络即使是对小数据集也能泛化的很好。
事实上,我们的网络已经比起初的(priori)期望好很多了。一个100个隐藏神经元的网络有尽80,000个参数。训练数据只有50,000张图片。就像试图用一个80,000次多项式来拟合50,000个数据点。不管怎样,我们的网络会过拟合的很厉害。然而,像之前看到的,这样的网络实际上泛化的还是很好的。为什么会这样呢?这不是很好理解。有推测说是“多层网络的动态梯度下降学习有一种'自泛化'的效果”【Yann LeCun, Léon Bottou, Yoshua Bengio, 和 Patrick Haffner 的 Gradient-Based Learning Applied to Document Recognition(1998)】。这是非常幸运的,但有些让人不安的是我们不理解为什么会这样。在此期间,我们将采用务实的策略,只要可以都会使用正则化。我们的神经网络将会泛化的更好。
让我们回到之前未解释的一个细节上,来结束本章:实事上L2正则化没有限制偏移量。当然很容易修改正则化过程来正则化偏移量。从经验上讲,这样做通常并不会改变多少结果,所从某种程度上讲这仅仅是一种习惯,是正则化偏移量还是不做。尽管这样,还是要注意,一个大偏移并不会像大权重样让神经元对输入敏感。因此我们不用去担心大偏移会让我们的网络从训练数据中学习到噪声。同时,允许大偏移让我们的网络有更强的灵活性——尤其是大偏移在某些期望的情况下,让神经元更容易饱和。因为这些原因我们通常不会在正则时,不会包含偏移量。