其他的正则化技术
除了L2正则外还有许多正则化技术。实际上,开发的技术多的不能都总结下来。在本节会简略讲三种减少过拟合的方法:L1正则,dropout,和人为增加训练集大小。我们不会像之前那样学习这些技术。相反,我们的目标是熟悉主要思想,并领会不同正则化技术的长处。
L1正则:这个方法是修改了非正则化成本函数,加上所有权重绝对值的和:
直觉上,这和L2正则很相似,惩罚大权重,并让网络更倾向于小权重。当然,L1正则项和L2的正则项是不同的,因此不应该期望会得到相同的效果。让我们试着去理解使用L1正则网络和用L2正则的有何不同。
这样做的话,先看一下成本函数的偏导数。对(95)做微分得到:
这里的是的符号,也就说,如果是正数则是,如果是负数那么就是。使用这个公式,我们可以很容易的用L1正则修改反向传播算法来做随机梯度下降。结果就是L1正则网络网络的更新规则变为
这里和往常一样,如果需要的话,可以用一个小批次的平均值来估计。对照L2正则的更新规则(转自公式(93)),
两个公式的正则效果都是为了缩小权重。这和我们的直觉是一致的,所有的正则化技术都对大权重进行惩罚。但缩小权重的方式不太一样。在L1正则中,是通过一个趋于0的常量。在L2正则中,是通过一个与成比例的量。因此当一个权重的量级很大时,,L1正则对权重的缩小将比L2正则小的多。相反,当比较小,L1正则对权重的缩小将比L2正则大的多。L1正则化网络的结果将趋向于浓缩高价值连接的权重到一个相对小的值,而其他权重趋向于0。
上面的讨论掩盖了一个问题,当的时候,偏导数是没有定义的。因为函数在处有一个“锐角”,所以在那一点是不可微的。不过,这没关系。当时,只要对随机梯度下降法用平常(非正则)的规则就可以了。这应该没问题——直观上,正则化的效果是缩小权重,显然当权重已经是0的话是没法再缩小的。为了表达地更准确,我们在公式(96)和(97)中约定。这样对L1正则下的随机梯度下降法来说有了一个漂亮简洁规则。
Dropout: Dropout是一个与其他正则化有本质区别的技术。不像L1和L2正则,dropout不依赖于修改成本函数。相反,在dropout里修改的网络本身。在解释它为什么起作用和它的效果之前,我们先看一下dropout的工作原理。
假设我们要训练一个网络:
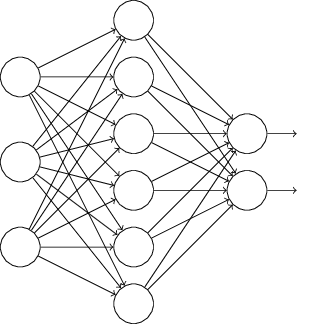
假定有一个训练输入和对应的期望输出。通常,我们的训练会通过网络向前传播x,然后反向传播确定对梯度的贡献。用dropout的话,这个流程要修改一下。开始先随机(临时地)删掉一半网络中的神经元,同时保留输入和输出神经元不受影响。这样做之后,我们将形成下面几条线的网络。注意被丢弃的神经元,也就是,这些神经元只是被暂时删掉,仍然以虚线的形式存在:

我们通过修改过的网络向前传播输入,然后也通过修改后的网络反向传播结果。这样在一个小批次样本上做完后,我们更新适当的权重和偏移量。然后重复这个过程,首先恢复被丢失的神经元,然后在隐含神经元中选择随机一个子集删除掉,再在一个不同的小批次上估算梯度,并更新网络上的权重和偏移量。
通过一遍又一遍的重复这个过程,我们的网络将学到一个权重和偏移量的集合。当然,这些权重和偏移量是在丢弃了一半隐含神经元的条件下学到的。实事上当我们运行整个网络时,意味着有两倍多的隐含神经元将是激活的。为了补偿这一点,我们把隐含神经元的权重减半。
这个dropout的过程可能看上去很奇怪而且很特别。为什么我们会期望它对正则化有帮助呢?为了解释事情的经过,建议你暂时别去考虑dropout,相反去想象用标准方式(非dropout)下是怎么训练神经网络的。尤其想象一下训练几种不同的神经网络,都用相同的训练数据。当然,网络可能不尽相同,将导致训练后的结果不太一样。当发生这样的事情后,我们可能用一些平均或投票机制来决定应该输出什么。举例来说,如果我们训练了5个网络,它们中的3个把一个数字分成“3”,那么它很可能就是一个“3”。其他2个网络可能是做错了。这种平均机制通常被发现是一个很强力的减少过拟合的方式(虽然代价有点高)。原因是不同网络可能过拟合的方式不一样,平均化可能会帮助消除这种过拟合。
这和dropout又有什么关系呢?当我们丢弃不同的神经元集合时,就很像是在试探着训练不同的神经网络。因此dropout的过程就像在均化大量不同网络的效果。不同的网络过拟合的方式不同,因此,dropout网络很有希望能减少过拟合。
一个dropout的相关启发式解释是在最早使用这项技术的论文里【ImageNet Classification with Deep Convolutional Neural Networks, 作者Alex Krizhevsky, Ilya Sutskever, 和Geoffrey Hinton (2012)】:“这项技术减少了神经元复杂性和相互适应性,因为神经元不能依赖其他已有的特定神经元。所以就强迫其学习更多鲁棒的特征,能帮助其与许多随机不同的其他神经元相结合。”换句话说,如果想让我们的网络做为预测的模型,那么可以把dropout当成是一种鲁棒到即使丢失个别证据也能正常工作的方式。对此,它与L1和L2正则很类似,都趋向于减小权重,因此网络能更鲁棒的丢弃网络里的任意个别连接。
当然,对dropout的真正评价是它已经非常成功的提升了神经网络的性能。论文原著【Improving neural networks by preventing co-adaptation of feature detectors 作者:Geoffrey Hinton, Nitish Srivastava, Alex Krizhevsky, Ilya Sutskever, 和Ruslan Salakhutdinov (2012)。注意论文中讨论了很多其微妙之外,这些我在简评中被忽略了。】介绍了这项应用于多种不同的任务。对我们来说,特别感兴趣的是他们应用dropout来做MNIST手写体分类时,用了一种平常的前馈神经元,这个我们已经考虑过类似的了。论文中指出使用这种架构在测试集上的分类准确率最高也就是98.4%.它们使用了dropout和修改过的L2正则的结合体将其提升到了98.7%。类似喜人的结果也在其他很多任务上得出,包括图片和语言识别,自然语言处理。Dropout在训练大,深的网络格外有用,它们的过拟合问题通常很严重。
人为扩展训练数据:我们之前看到当只用1,000个训练图片时,我们的MNIST分类准确率下降到80%左右。这种情况没有什么好惊讶的,因为训练数据少意味着我们的网络只会接触更少的人类书写数字的方式。让我们尝试用有各种不同训练数据集的大小,来训练30个隐含神经元的网络,来看看性能的变化。训练用的小批次大小为10,学习率为,正则参数,成本函数为交叉熵。当用全训练数据集时训练30代,当用小训练数据时用按比例缩小的代数。为了保证权重衰弱因子在训练数据集间保持一致,当用全训练数据集时正则参数,当使用小训练数据集时按比例缩小【这个和下面两幅图片是使用程序more_data.py做的】。
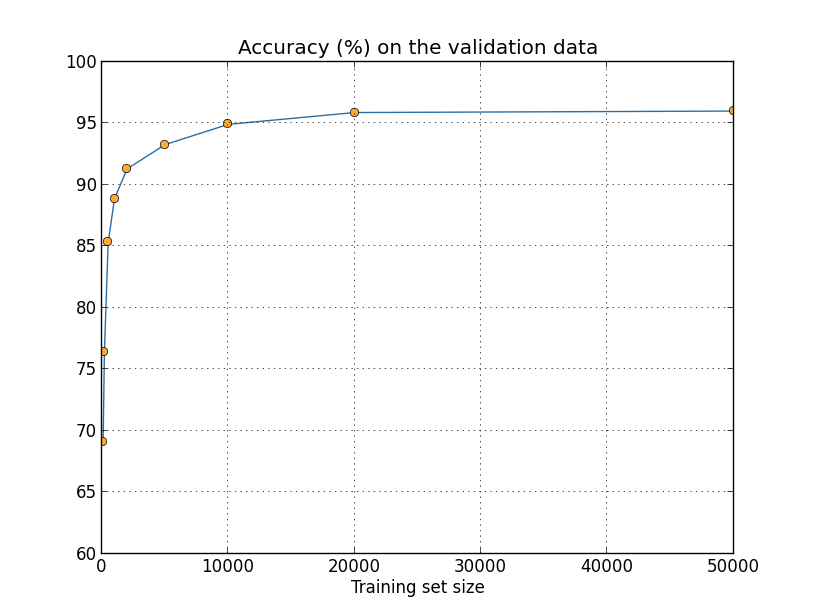
正如你所看到的,当使用更多训练数据时分类准确率有显著提升。如果有更多数据的话想必会有进一步的提升。当然,从上图来看差不多已经接近饱和了。尽管这样,假使用对数方式来表示训练集大小的话,图片将会是下面这样:
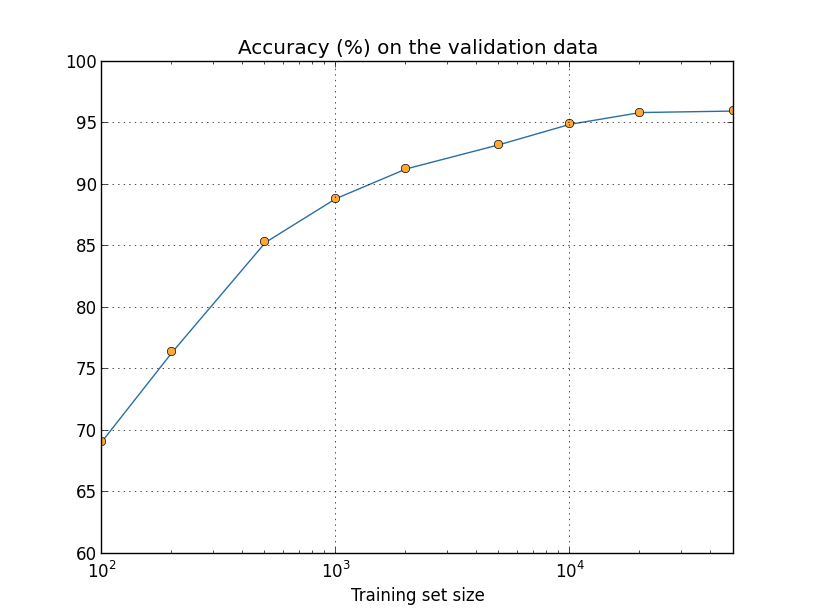
明显能看到图片在结果时还在攀升。这样假设如果用更多的训练数据——比如说,百万或甚至十亿的手写样本,而不是只有50,000——那么我们可能会得到明显更好的性能,即使是在这个很小的网络上。
获得更多的训练数据的主意不错。不幸的是,代价很昂贵,因此实事上并不总是可行。尽管这样,还是有别外一个差不多好的做法,就是人为扩展训练数据。例如,假设我们拿到一个NMIST训练数据中的五:

然后轻轻的旋转,比如说15度:

它仍是相同的数字。然而在像素层面上它和其他NMIST训练数据中的图片有很大差异。可以想象添加这些图片到训练数据中会帮助我们的网络更好的学习分类数字。此外,显然不很于只是添加这一个图片。我们可以通过在所有MNIST训练图片上都做小量旋转来扩展训练数据,然后用这些扩展后的训练数据提升网络的性能。
这个作法很有用,被应用的很广泛。让我们从一篇论文中看一些结果【Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis作者 Patrice Simard, Dave Steinkraus, 和John Platt (2003)】,里面对MNIST使用了多种方法的变种。它们考虑过的一种神经网络架构与我们使用的很类似,有800个隐含神经元的前馈网络,使用交叉熵成本函数。使用标准的MNIST训练数据跑这个网络,他们在其测试集上达到了98.4%的分类准确率。但他们扩展了训练数据,不只是上面说的旋转,还有平移和偏移图片。通过在扩展数据集上训练,他们将准确率提升到了98.9%。他们也尝试了叫做“弹性变形”,一种特殊的图片变形类型,用来描述手部肌肉的随机振荡。通过使用弹性变形来扩展数据,他们达到超高的99.3%的准确率。他们通过显露在真实手写发现的变化,从而有效的扩展了网络的性能。
这种做法的变种可以被用来提升许多学习任务的性能,不只是手写识别。一般原则是通过应用反应真实世界变化相关的操作来扩展训练数据。想出这种做法的方式并不难。例如,假设你要构建一个做语音识别的网络。我们人类即使在失真的情况下也可以对语音进行识别,例如环境噪音。因此你可以通过添加环境噪音来扩展数据。我们也可以在语速加快或减慢的情况下识别语音。因此这是另外一种扩展训练数据的方式。这些技术并不总会用到,比如,替代添加噪音来扩展训练数据的是,可以在网络前面加一个减少噪音的过滤器来清理输入,可能会效果会更好。它仍然值得你去保留这种扩展数据的想法,并寻找契机应用它。
练习
- 像上面讨论的,一种扩展MNIST训练数据的方式是在训练图片上做一个小的旋转。那如果在训练图片上允许任意大角度的旋转会发生什么问题呢?
除了数字大之外,比较分类准确率的意义是什么: 让我们再看一下神经网络准确率随着训练集大小的变化:

假设用其他机器学习技术分类数字来替代神经网络。例如,让我们尝试用第一章简单接触过的支持向量机(SVM)。和第一章的情况一样,如果你对SVM不熟悉的话也不用担心,我们不需要去理解它们的细节。反而我们会直接用scikit-learn库提供的SVM。这里是SVM性能随训练集大小的变化。为了比较方便,我也将这个神经网络的结果绘制了出来【这张图片是用程序more_data.py生成的(和前面几张一样)】:
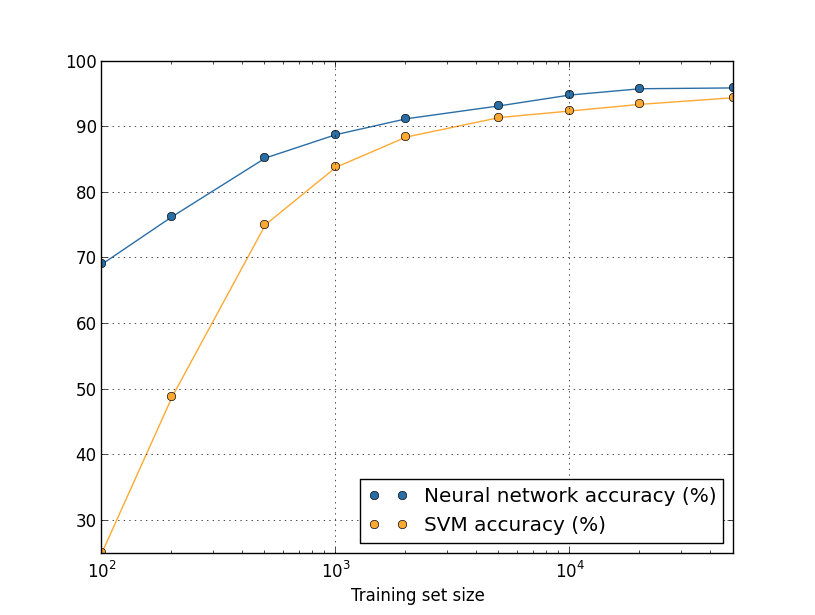
可能这张图首先让你想到是我们的神经网络在每个训练集大小上的都要胜过SVM。这很好,但请不要过度解读,因为我只是用了scikit-learn中SVM开箱即用的初始配置,然而我们做了许多工作来提升我们的神经网络。这张图有一个很微妙但非常有趣的实事是,如果我们用50,000张图片训练SVM,准确率(94.48%的准确率),比我们的神经网络用5,000张图片(93.24%的准确率)时要好。换句话说,用更多的训练数据有可以补偿所使用机器学习算法上的差距。
甚至会发生更有意思的事情。假设我们尝试用两种机器学习算法来解决一个问题,算法A和算法B。有时会发生算法A在一个训练数据集上胜过算法B,然后算法B在不同的训练数据集上要强过算法A。在上面的图片中看不到——它需要两个图片交叉——但确实发生了【明显的例子在Scaling to very very large corpora for natural language disambiguation中,作者Michele Banko和Eric Brill (2001) 】。问题“算法A比算法B好吗?”的正确答复是:“你用什么样的训练数据”。
所有这些都是在做开发和读论文时要注意的。许多论文都集中在寻找新技巧来榨取标准数据集上的性能提升。“我们杰出的技术让我们在标准数据Y上提升了X%的性能”是一种典型的研究声明。这种声明通常确实值得关注,但一定理解它们只是在用特定训练数据集的背景下才得出来。想象下另一种历史,那个最初创建基础数据集的人有比别人更多的研究经费。它们可能会用这笔额外的钱来收集更多的训练数据。这就完全有可能在一个更大的数据集上因牛逼的技术而得到“改进”。换句话说,这种传说中的改进可能只是历史上的偶然。我想表达的意思上,尤其是在特定的应用中,更好的算法和更好的训练数据都是我们想要的。寻找更好算法没有问题,但确保你别只是把注意力集中在更好的算法上,而排除了那些容易获得更多或更好的训练数据。
问题
- (研究问题)我们的机器学习算法在超大数据集极限情况下会怎样?对于任何给定的算法,在真正的大数据极限下,很自然的会去尝试去定义一个近似性能的概念。对这个问题一个快而拙劣的方法是简单的尝试去拟合像上面图像上的曲线,然后推测拟合曲线到无穷大。这个方法有一个缺陷就是不同方法的曲线拟合将给出不同的近似性能的概念。你可以找一个拟合某一特定类别曲线的准则吗?如果可以,比较下多种不同机器学习算法的近似性能。
总结:我们现在已经完成对过拟合和正则化的研究。当然,我们将再次回到这个问题。正如我多次提及的,过拟合是神经网络的一个主要问题,尤其是计算机越发强大,有能力去训练更大的网络。因此,迫切需要开发强大的正则化技术来减少过度拟合,这也是当前工作中极其活跃的领域。