权重初始化

当我们创建神经网络时，必须要选出初始的权重和偏移量。到目前为止，我们是按照之前第1章简短描述过的一个惯例来选的。只是提醒你，这个惯例选权重和偏移量都是用独立高斯随机变量，归一化成均值为0、标准差为1。虽然这种方法很有效，但是临时方案，它值得我们回头看看是否能找到一个更好方案来设置初始的权重和偏移量，也许能让我们的神经网络学习的更快。

事实证明，我们可以做的比用归一化高斯函数初始化好的多。为说明原因，假设我们的网络里大量输入神经元——比如说1,000个。然后，假设已经用归一化高斯函数初始化的与第一个隐藏层的权重。到目前为止，我会将权重特别压缩至输入层到第一个隐藏层，忽略网络剩余的其他层：

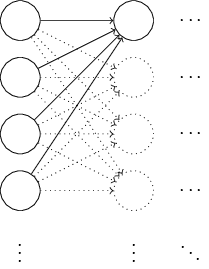
简单起见，假设我们试着用一个训练输入x来训练，其中一半的输入神经元是开的，也就是设置成1，一半输入神经元是关的，也是就设置成0。下面的论点更具普遍性，但你会从这个特例中得到其要点。让我们考虑下输入到隐藏神经元的权重和 $z = \sum_j w_j x_j+b$ 。和里的500项被消掉了，因为对应的输入 $x_j$ 是0。因此 $z$ 总共是501个归一化高斯函数随机变量的和，包括500个权重项和1个额外的偏移量项。因此 $z$ 本身是一个均值为0，标准差为 $\sqrt{501} \approx 22.4$ 的高斯分布。也就是说， $z$ 是一个非常宽的高斯分布，根本没有尖峰：

尤其是，我们可以从这张图上看到很可能 $|z|$ 相当的大，也就是说要不 $z \gg 1$ ，要不 $z \ll -1$ ；如果那样的话，隐藏神经元的输出 $\sigma(z)$ 将会非常接近1或0。这就意味着我们的隐藏神经元将会饱和。当这种情况发生时，正如我们所知道的那样，在权重中做出微小的改变只会使我们激活的隐藏神经元发生极小的变化。激活的隐藏神经元的这种微小改变，反过来又几乎不会影响到整个网络中其余的神经元，然后只在成本函数里看到一个相应微小的改变。结果就是，这些权重在用梯度下降算法时，只会学习的非常缓慢【在第2章详细的讨论了更多细节，那里我们用反向传播公式展示了，饱和神经元的权重输入学习缓慢】。这跟本章之前讨论的问题很相似，输出神经元在错误的值上饱和导致学习缓慢。之前的问题我们是用精巧的成本函数解决的。不幸的是，虽然它对饱和输出神经元有效，但对饱和的隐藏神经元一点用都没有。

我一直在讲输入层到第一个隐藏层的权重。当然，类似的观点也适应于后面的隐藏层：如果后面隐藏层的权重初始化用的是归一化的高斯函数，那么激活值将经常非常接近0或1,学习又将非常缓慢。

那有没有什么方法可以选到更好的初始权重和偏移量，让我们不再遇到这种类型的饱和，避免学习缓慢？假设有一个神经元的输入权重为 $n_{\rm in}$ 。那将这些权重初始化成均值为0，标准差为 $1/\sqrt{n_{\rm in}}$ 的高斯随机变量。也就是说，我们将把高斯函数压下去，这样我们的神经元就不太可能饱和。我们将继续用均值为0，标准差为1的高斯函数来选择偏移量，原因过会再讲。这样选之后，权重和 $z = \sum_j w_j x_j + b$ 将再一次是均值为0的高斯随机变量，但要比之前陡的多。假设像之前那样，500个输入是0，500个输入为1.那么很容易看到（见下面的练习） $z$ 具有均值为0，标准差为 $\sqrt{3/2} = 1.22\ldots$ 的高斯分布。这比之前陡多了，即使下面的图也低估了情况，因此与之前图进行比较时，不得不对垂直轴做缩放：

这样的神经元不太可能饱和，相应的也不太可能出现学习缓慢的问题。

练习

证明上面段落中 $z = \sum_j w_j x_j + b$ 的标准差为 $\sqrt{3/2}$ 。了解下面这些或许会有帮助：(a)独立随机变量和的方差就是单个随机变量方差的和；(b)方差就是标准差的平方。

我上面说将继续像之前那样初始化偏移量，用均值为0，标准差为1的高斯随机变量。这样是没问题的，因为它不太像会让神经元饱和。实事上，如何初始化偏移量没什么所谓，只要我们避免了饱和问题。有些人甚至把所有的偏移量都初始化为0，并依靠梯度下降来学习适当的偏移量。但因为不太可能有很大差别，我们将继续沿用之前的初始化方式。

让我们用MNIST数字分类任务来比较一下新老权重初始化方法。像之前一样，用30个隐藏神经元，小批次大小为10，正则参数 $\lambda = 5.0$ ，成本函数为交叉熵。我们将微微减小学习率由 $\eta = 0.5$ 改为 $\eta = 0.1$ ，因为这样可以让图片里的结果更容易显现出来。我们可以用老的权重初始化方法来训练：

>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,
... evaluation_data=validation_data, 
... monitor_evaluation_accuracy=True)

我们也可心用新的权重初始化方法来训练。这实际上更简单，因为network2的默认权重初始化就是用的新方法。这就意味着我们可以忽略上面的net.large_weight_initializer()函数调用：

>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,
... evaluation_data=validation_data, 
... monitor_evaluation_accuracy=True)

结果绘制出来就是：【生成这个和下面图片的程序为weight_initialization.py】

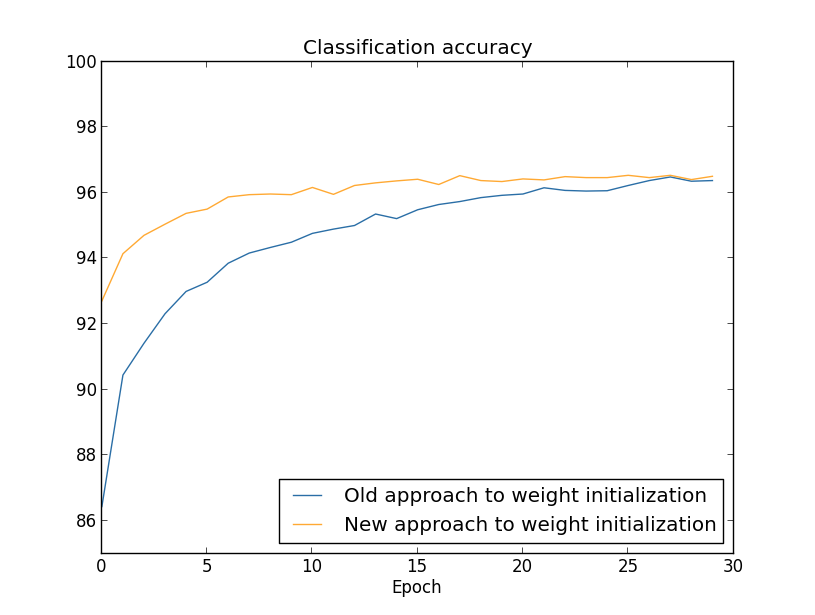
在这两种情况下，分类准确率都超过了96%。两者的最终分类准确率几乎差不多。但新的初始化技术更快地达到。在第一代训练结束后，老的权重初始化方法的分类准确率在87%以下，而新的方法已经超过93%了。似乎新的权重初始化方法让我们从更好的态势下开始，从而能更快的达到好的结果。如果绘制100个神经元的结果也能看到相同的现象：

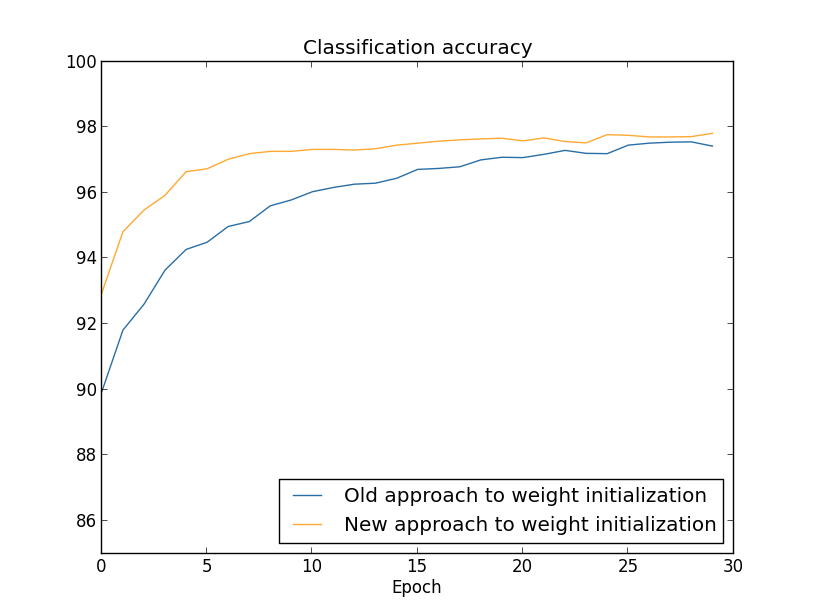
这种情况下，两条曲线没有相交。然而，我的试验表明只要再做几代的训练（没有显示出来）准确率就几乎一样了。因此，从这些试验中可以看到，权重初始化的改进只是加快了学习速度，并不会改变网络最终的性能。可在第4章里会看到一些神经网络的例子，用 $1/\sqrt{n_{\rm in}}$ 的权重初始化的长期行为明显更好。因此，它并不是只对学习速度有提升，有时也影响最终性能。

$1/\sqrt{n_{\rm in}}$ 的权重初始化方法对神经网络学习的提升是有帮助的。也提出一些其他的权重初始化技术，很多都是基于这个基本思想。这里我就不看其他技术了，因为 $1/\sqrt{n_{\rm in}}$ 对我们来说已经很好用了。如果你有兴趣做更深入了解地话，建议你看一下2012看Yoshua Bengio论文14至15页的探讨，【Practical Recommendations for Gradient-Based Training of Deep Architectures 作者Yoshua Bengio(2012)】，以及其中的参考文献。

问题

正则化与改进权重初始化方法的联系 L2正则有时会自动给出一些与新权重初始化方法相似的东西。假设我们用老方法来初始化权重。简述一个可探究的观点：(1)假如 $\lambda$ 不是太小，第一代的训练几乎将被权重衰退支配；(2)假如 $\eta \lambda \ll n$ 权重将以每代 $\exp(-\eta \lambda / m)$ 的系数衰退；(3)假如 $\lambda$ 不是太大，权重衰退将会在权重下降至 $1/\sqrt{n}$ 附近时减弱，这里 $n$ 是网络里权重的总数量。我认为这些条件在本节的样例图像中都是满足的。

权重初始化

权重初始化

练习

问题

results matching ""

No results matching ""