反向传播：概览

就像我已阐述的，反向传播有两个迷团。首先，这个算法到底做了些什么事情？我已经做了一张误差从输出层进行反向传播的图片。但我们是否能更深入一些，更直观的构建当这些矩阵和向量相乘时的后续？第二个迷团是一个人怎样能在最开始的时候发现反向传播算法？有件事是知道算法的步骤，及至知道算法的的证明过程。但这并不意味着理解问题就可以在最开始的时候能发现这个算法。是否有一种合理的解释可以引导我们发现反向传播算法？这一章将讨论这些谜团。

为了让算法的工作过程更加直观，想象我们在网络的一个权重$w^l_{jk}$上增加了一个小小的改变$\Delta w^l_{jk}$：

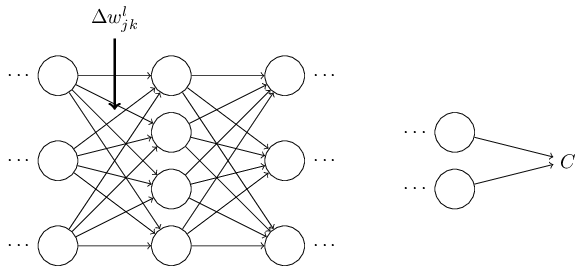
这个权重的变化导致相关神经元输出的激活值发生了改变：

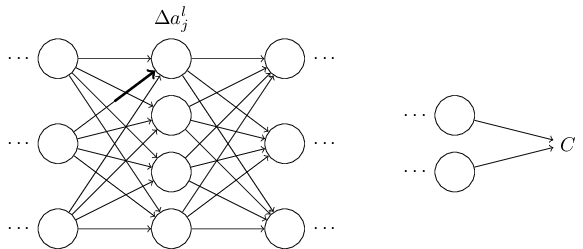
这将依次导致下面网络层所有激活值的发现改变：

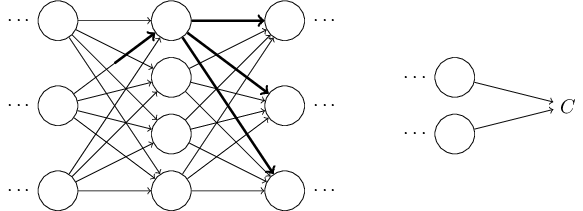
那些改变将依次引起下一层，和下下层，和所有到最终层引路上所有网络层发生改变，直到成本函数：

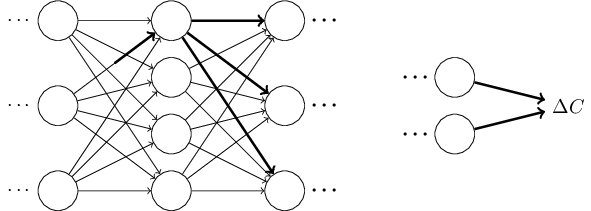
成本的改变$\Delta C$通过下面这个等式与权重的改变$\Delta w^l_{jk}$相关联：

$\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial w^l_{jk}} \Delta w^l_{jk}. \tag{47} \end{eqnarray}$

这个等式表明计算$\frac{\partial C}{\partial w^l_{jk}}$的一种可能的方法是仔细追踪$w^l_{jk}$的小小改变是怎样传播引起$C$的变化的。如果我们能做到这个，在容易计算的情况下，仔细将引路所有的东西表示出来，那么应该可以计算${\partial C} / {\partial w^l_{jk}}$。

让我们尝试做一下。改变$\Delta w^l_{jk}$引起$l^{th}$层第$j^{th}$个神经元的改变$\Delta a^l_j$。这个改变由下面给出：

$\begin{eqnarray} \Delta a^l_j \approx \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}. \tag{48}\end{eqnarray}$

激活值$\Delta a^l_j$的改变将下一层所有激活值的变化，如，第$(l+1)^{th}$层。我们将只集中于其中一个激活值的影响范围，比方说，$a^{l+1}_q$，

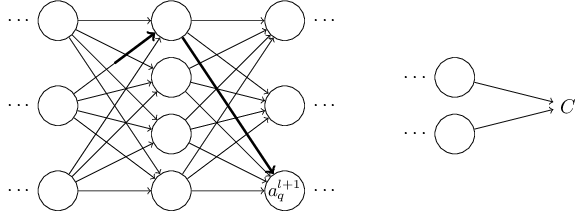
实际上，这将引起下面的改变：

$\begin{eqnarray} \Delta a^{l+1}_q \approx \frac{\partial a^{l+1}_q}{\partial a^l_j} \Delta a^l_j. \tag{49}\end{eqnarray}$

用等式(48)做公式代换，得到：

$\begin{eqnarray} \Delta a^{l+1}_q \approx \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}. \tag{50}\end{eqnarray}$

当然，$\Delta a^{l+1}_q$的改变将依次改变下一层的激活值。实际上，我们可以想象一条从$w^l_{jk}$至$C$贯穿网络所有通道的路径，其中的每个激活值的改变引起下一层激活值的变化，最终至输出层成本的变化。如果这条路径穿过了激活值$a^l_j, a^{l+1}_q, \ldots, a^{L-1}_n, a^L_m$，那它的结果表达示为

$\begin{eqnarray} \Delta C \approx \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}, \tag{51} \end{eqnarray}$

即，从每个穿过的神经元中抽取一个${\partial a}/{\partial a}$类型的式子，最后也是同样类型的式子${\partial C}/{\partial a^L_m}$。这代表$C$的改变是由于这条贯穿网络的特定路径上激活值的改变。当然，$w^l_{jk}$的变化有很多条路径可以传播至影响成本，但我们一直在考虑单条路径的情况。为了计算$C$的总改变，看起来可以将权重和最终成本间所有可能的路径做汇总求知，也就是，

$\begin{eqnarray} \Delta C \approx \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}} \Delta w^l_{jk}, \tag{52} \end{eqnarray}$

这里对路径上所有可能选择的中间神经元进行了求和。与(47)比较可以发现

$\begin{eqnarray} \frac{\partial C}{\partial w^l_{jk}} = \sum_{mnp\ldots q} \frac{\partial C}{\partial a^L_m} \frac{\partial a^L_m}{\partial a^{L-1}_n} \frac{\partial a^{L-1}_n}{\partial a^{L-2}_p} \ldots \frac{\partial a^{l+1}_q}{\partial a^l_j} \frac{\partial a^l_j}{\partial w^l_{jk}}. \tag{53} \end{eqnarray}$

现在，等式(53)看起来很复杂。尽管如此，它有一个很直观的解释。我们计算的是网络里$C$关于权重的变化率。这个等式告诉我们，网络中神经元之间的每条边与一个变化率因子相关，就是一个神经元激活值关于另一个神经元激活值的偏导数。从首个权重至首个神经元边的变化率因子是$\partial a^{l}_j / \partial w^l_{jk}$。一条路径的变化率因子就是路径上所有变化率因子的积。并且，$\partial C / \partial w^l_{jk}$的总变化率就是从初始权重至最终成本间所有路径变化率因子的和。下面演示了单路径下的这个过程：

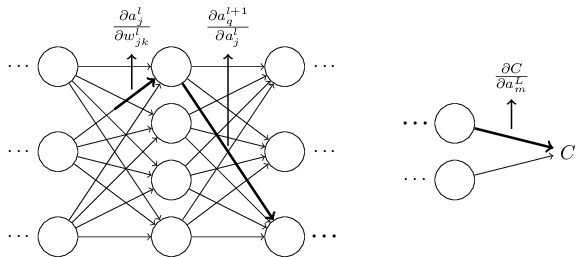
目前为止提供的是一个启发式的论点，思考的方式是当你扰乱网络中的一个权重时会发生什么事情。让我们来草拟一个可以发展这个论点的思路。首先，你需要对等式(53)中所有单个偏导数导出显示表达式。这通过一点计算就很容易做到。完成后，你再尝试想出一种方式将所有的相加项的索引写成矩阵乘法的形式。这将变得很乏味，并需要一些毅力，但不需特别的洞察力。做完所有这些之后，然后尽可能的进行简化，最后你会发现这恰好就是反向传播算法！因此你可以将反向传播算法看成是提供了一种计算所有这些路径上变化率因子和的方式。或者，稍微有些不同的说法，反向传播算法是一种很聪明的方式来跟踪权重（和偏移量）的扰动在网络中的传播，到达输出层，并影响成本。

现在，我将不会将所有这些做出来。它很凌乱，而且需要相当仔细来解决所有这些细节。如果你打算挑战一下，你应该会蛮喜欢这次尝试。如果不是，希望这个思路能在反向传播的实现上带来一些启发。

另一个迷团怎么样——起初是怎样发现反向传播的呢？实际上，如果你理顺了我刚刚描述的方法，你将发现反向传播的证明。不幸的是，这个证明比较长并且要比本章早些时候描述的要复杂的多。所以这个短的（但更神秘）证明是怎样被发现的呢？当你将这个长证明的所有细节写出来后，你会发现有很多一眼就可以看出来的简化方式。你应用了这些简化，得出了一个较短的证明，然后写出来。然后你又会发现很多显而易见的简化方式。然后你再做一次。经过几次迭代后的结果就是我明早些时候看到的证明【需要一个聪明的步骤。等式(53)的中间变量是像$a^{l+1}_q$这些的激活值。聪明的想法是将其替换为使用权重输入作为中间变量，就像$z^{l+1}_q$。如果你没想到这个点子，继续使用激活值$a^{l+1}_q$，证明过程将比本章先前的要复杂很多。】——简短，但有点模糊，因为所有那些有用的指示都被移除了！当然，请相信我，早些时候的证明原来并没有什么神秘之处。它只是本章中描述的大量艰辛的简化工作。